در نظریه محاسبات ونظریه اتوماتا , ساختمان پاورست یا زیر مجموعه ساختمان یکی از روش های تبدیل کردن یک اتوماتون تعین ناپذیر متناهی ( NFA ) به ماشین های تعین پذیر حالات متناهی ( DFA ) می باشد که شبیه تشخیص زبان صوری می باشد. در این نظریه خیلی مهم است زیرا که براساس NFA بناشده است اگر چه انعطاف پذیری زیادی دارد ولی قادر به شناسایی تمام زبان هایی که توسط DFA شناسایی می شود نیست. به بیان دیگر NFA انعطاف پذیری زیادی دارد اما چون بعضی از زبان ها را قادر به تبدیل به DFA نیستند را نمیتوان به صورت فرمولی در آورد بخاطر همین کاراییش کمتر از DFA هست حتماً باید تبدیل شود تا بتوان گفت فرمولی برایش وجود دارد.
این خیلی مهم است برای تمرین تبدیل کردن ساختار آسان تر NFA به DFA بسیار کارآمد انجام پذیرد در حالی که اگر , n ایستگاه دارد , نتیجه تبدیل به DFA می تواند 2n ایستگاه داشته باشد , یک عدد بزرگ نمایی که بعضی از اوقات ساختار غیر عملی برای NFA های بزرگ می شود ( نمی شود تبدیل کرد ) .
این ساختار , بعضی اوقات Rabin–Scott powerset construction یا زیر مجموعهٔ ساختار نامیده می شود. تا با این واسطهٔ متمایزی بین ساختارهای متشابه برای نوع های دیگر از اتوماتون قائل شونند که اولین بار توسط مایکل رابین و دانا اسکات در 1995 بیان شد.
ساختمان پاورست به طور مستقیم به NFA اعمال می شود بطوری که تغییرات حالت، بدون مصرف نمادهای ورودی ( با نام " ε - moves " ) اجازه نمی دهد. چنین ماشینی می تواند به عنوان 5 - عنصر ( Q, Σ, T, q0, F ) در نظر گرفته شود که در آن Q مجموعه ای از حالات تعریف شده است، Σ مجموعه ای از نمادهای ورودی، T تابع انتقال ( که یک حالت و نماد ورودی را به یک مجموعه از حالت ها می نگارد، q0 حالت اولیه است و F مجموعه ای از حالات پذیرش است. DFA مربوطه، حالاتی که زیر مجموعه Q می باشد را داراست . حالت اولیه برای ماشین های تعین پذیر حالات متناهی , { q0} می باشد که مجموعه ای تک عضوی از حالات اولیه است. تابع انتقال DFA حالت S را ( به نمایندگی از یک زیر مجموعه از Q ) وسمبل ورودی X را به مجموعه { T ( S, x ) = ∪{T ( q, x ) | q ∈ S می نگارد، مجموعه ای از همه حالات که می تواند با گذارX از حالت در S تحقق یابد. حالتS از DFA حالت پذیرا است اگر و تنها اگر حداقل یک عضو S یک حالت پذیرا از NFAباشد.
NFA زیر دارای 4 حالت است. حالت 1 , حالت اولیه است و حالت 3 و 4 حالت پذیرفته شده است. الفبای آن شامل 2 نماد 0 و1 است. و دارای ε - moves است. حالت 1 , حالت اولیه است.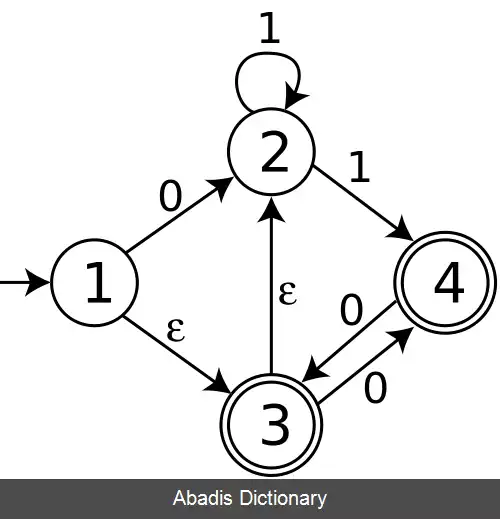
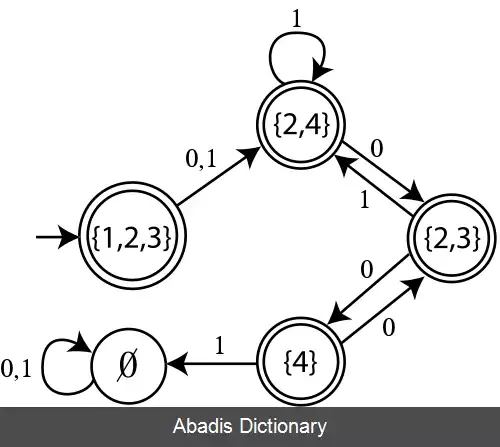
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین خیلی مهم است برای تمرین تبدیل کردن ساختار آسان تر NFA به DFA بسیار کارآمد انجام پذیرد در حالی که اگر , n ایستگاه دارد , نتیجه تبدیل به DFA می تواند 2n ایستگاه داشته باشد , یک عدد بزرگ نمایی که بعضی از اوقات ساختار غیر عملی برای NFA های بزرگ می شود ( نمی شود تبدیل کرد ) .
این ساختار , بعضی اوقات Rabin–Scott powerset construction یا زیر مجموعهٔ ساختار نامیده می شود. تا با این واسطهٔ متمایزی بین ساختارهای متشابه برای نوع های دیگر از اتوماتون قائل شونند که اولین بار توسط مایکل رابین و دانا اسکات در 1995 بیان شد.
ساختمان پاورست به طور مستقیم به NFA اعمال می شود بطوری که تغییرات حالت، بدون مصرف نمادهای ورودی ( با نام " ε - moves " ) اجازه نمی دهد. چنین ماشینی می تواند به عنوان 5 - عنصر ( Q, Σ, T, q0, F ) در نظر گرفته شود که در آن Q مجموعه ای از حالات تعریف شده است، Σ مجموعه ای از نمادهای ورودی، T تابع انتقال ( که یک حالت و نماد ورودی را به یک مجموعه از حالت ها می نگارد، q0 حالت اولیه است و F مجموعه ای از حالات پذیرش است. DFA مربوطه، حالاتی که زیر مجموعه Q می باشد را داراست . حالت اولیه برای ماشین های تعین پذیر حالات متناهی , { q0} می باشد که مجموعه ای تک عضوی از حالات اولیه است. تابع انتقال DFA حالت S را ( به نمایندگی از یک زیر مجموعه از Q ) وسمبل ورودی X را به مجموعه { T ( S, x ) = ∪{T ( q, x ) | q ∈ S می نگارد، مجموعه ای از همه حالات که می تواند با گذارX از حالت در S تحقق یابد. حالتS از DFA حالت پذیرا است اگر و تنها اگر حداقل یک عضو S یک حالت پذیرا از NFAباشد.
NFA زیر دارای 4 حالت است. حالت 1 , حالت اولیه است و حالت 3 و 4 حالت پذیرفته شده است. الفبای آن شامل 2 نماد 0 و1 است. و دارای ε - moves است. حالت 1 , حالت اولیه است.


wiki: ساختمان پاورست
