در نظریه گروه ها، اگر زیر مجموعهای از گروه G مانند H تحت عمل دوتایی تعریف شده بر G بسته بوده و خود H با آن عمل تعریف شده بر گروه G، گروه باشد آنگاه گوییم H زیرگروه G است.
فرض کنید ( • , G ) گروه باشد. زیرمجموعهٔ H از G را زیرگروه G گوییم اگر ( • , H ) گروه باشد. در اینصورت می نویسیم H ≤ G یا G ≥ H. همچنین H < G یا G> H به این معناست که H ≤ G و H ≠ G.
هر گروه G زیرگروه خودش است و اگر e عنصر همانی گروه باشد، آنگاه {e} نیز یک زیرگروه G است. این دو زیرگروه را زیرگروه های بدیهی G می نامیم.
اگر Z مجموعه اعداد صحیح و R مجموعه اعداد حقیقی باشد آنگاه ( Z , + ) < ( R , + ) .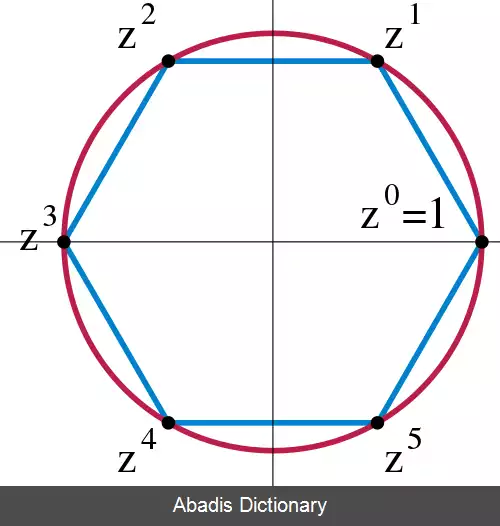
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنید ( • , G ) گروه باشد. زیرمجموعهٔ H از G را زیرگروه G گوییم اگر ( • , H ) گروه باشد. در اینصورت می نویسیم H ≤ G یا G ≥ H. همچنین H < G یا G> H به این معناست که H ≤ G و H ≠ G.
هر گروه G زیرگروه خودش است و اگر e عنصر همانی گروه باشد، آنگاه {e} نیز یک زیرگروه G است. این دو زیرگروه را زیرگروه های بدیهی G می نامیم.
اگر Z مجموعه اعداد صحیح و R مجموعه اعداد حقیقی باشد آنگاه ( Z , + ) < ( R , + ) .

wiki: زیرگروه
