زاویه داخلی یا زاویه داخلی چندضلعی ( به انگلیسی: Internal angle ) نوعی از زاویه است که در مورد اندازه گیری زاویه درون چندضلعی منتظم به کارگیری می رود.
زاویه خارجی ( به انگلیسی: External angle ) نوعی دیگر از زاویه است که در مورد اندازه گیری زاویه بیرون چندضلعی منتظم به کار می رود.
• در زاویه داخلی هرچقدر تعداد ضلع ها بیشتر شود، اندازه زاویه داخلی بیشتر می شود.
• در زاویه خارجی هرچقدر تعداد ضلع ها بیشتر شود، اندازه زاویه خارجی کمتر می شود.
• اگر زاویه داخلی را با زاویه خارجی جمع کنیم، برابر با°۱۸۰درجه می شود.
• زاویه داخلی و زاویه خارجی باهم مکمل هستند.
• مجموع زاویه هایی خارجی چندضلعی منتظم٬همیشه برابر با°۳۶۰درجه است
• مجموع زاویه های داخلی بستگی به تعداد ضلع چندضلعی منتظم دارد
• مثلث متساوی الاضلاع تنها چندضلعی منتظم است که زاویه خارجی او بیشتر زاویه داخلی اش می باشد
• مجموع زاویه داخلی یک مثلث برابر است با°۱۸۰درجه.
• مربع تنها چندضلعی منتظم است که زاویه داخلی او برابر با زاویه خارجی او است.
یک nضلعی منتظم را درنظر بگیرید.
ابتدا تعداد مثلث هایش را طبق چندضلعی های معروف محاسبه می کنیم
• مربع:۲مثلث
• پنج ضلعی منتظم:۳مثلث
• شش ضلعی منتظم:۴مثلث
• هفت ضلعی منتظم:۵مثلث
• هشت ضلعی منتظم:۶مثلث
• نه ضلعی منتظم:۷مثلث
• ده ضلعی منتظم:۸مثلث
طبق این الگو، متوجه می شویم که تعداد مثلث ها از تعداد ضلع های چندضلعی های منتظم دوتا کمتر است. پس تعداد مثلث درون هر چندضلعی منتظم برابر با این رابطه است.
تعداد مثلث: n − 2
چون مجموعه زاویه هایی داخلی یک مثلث°۱۸۰درجه است پس مجموعه زاویه هایی داخلی بر اساس مجموع زاویه های تعداد مثلث های دورن او است.
مجموع زاویه داخلی: 180 ( n − 2 )
اندازه زاویه داخلی چندضلعی منتظم برابر با تقسیم تعداد ضلع ها است. چون تعداد راس ها با تعداد ضلع ها برابر است.
اندازه هرزاویه داخلی: 180 n ( n − 2 )
مجموع زاویه خارجی هر چندضلعی منتظم برابر با۳۶۰ درجه است. پس برای اندازه گیری زاویه خارجی باید ۳۶۰ درجه به تعداد اضلاع چندضلعی منتظم تقسیم کنیم، تا اندازه زاویه آن مشخص گردد.
مجموع زاویه خارجی:360درجه
اندازه زاویه مجموع زاویه خارجی هر چندضلعی منتظم برابر با۳۶۰ درجه است. پس برای اندازه گیری زاویه خارجی باید ۳۶۰ درجه به تعداد اضلاع چندضلعی منتظم تقسیم کنیم، تا اندازه زاویه آن مشخص گردد.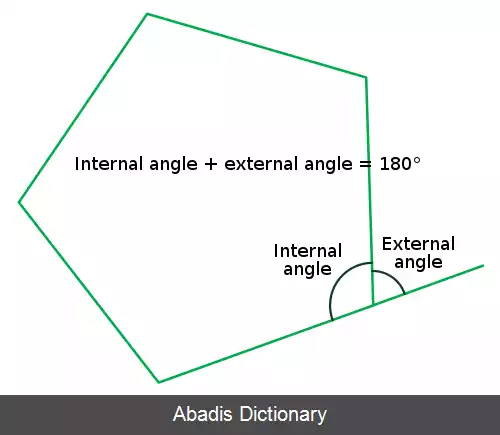
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفزاویه خارجی ( به انگلیسی: External angle ) نوعی دیگر از زاویه است که در مورد اندازه گیری زاویه بیرون چندضلعی منتظم به کار می رود.
• در زاویه داخلی هرچقدر تعداد ضلع ها بیشتر شود، اندازه زاویه داخلی بیشتر می شود.
• در زاویه خارجی هرچقدر تعداد ضلع ها بیشتر شود، اندازه زاویه خارجی کمتر می شود.
• اگر زاویه داخلی را با زاویه خارجی جمع کنیم، برابر با°۱۸۰درجه می شود.
• زاویه داخلی و زاویه خارجی باهم مکمل هستند.
• مجموع زاویه هایی خارجی چندضلعی منتظم٬همیشه برابر با°۳۶۰درجه است
• مجموع زاویه های داخلی بستگی به تعداد ضلع چندضلعی منتظم دارد
• مثلث متساوی الاضلاع تنها چندضلعی منتظم است که زاویه خارجی او بیشتر زاویه داخلی اش می باشد
• مجموع زاویه داخلی یک مثلث برابر است با°۱۸۰درجه.
• مربع تنها چندضلعی منتظم است که زاویه داخلی او برابر با زاویه خارجی او است.
یک nضلعی منتظم را درنظر بگیرید.
ابتدا تعداد مثلث هایش را طبق چندضلعی های معروف محاسبه می کنیم
• مربع:۲مثلث
• پنج ضلعی منتظم:۳مثلث
• شش ضلعی منتظم:۴مثلث
• هفت ضلعی منتظم:۵مثلث
• هشت ضلعی منتظم:۶مثلث
• نه ضلعی منتظم:۷مثلث
• ده ضلعی منتظم:۸مثلث
طبق این الگو، متوجه می شویم که تعداد مثلث ها از تعداد ضلع های چندضلعی های منتظم دوتا کمتر است. پس تعداد مثلث درون هر چندضلعی منتظم برابر با این رابطه است.
تعداد مثلث: n − 2
چون مجموعه زاویه هایی داخلی یک مثلث°۱۸۰درجه است پس مجموعه زاویه هایی داخلی بر اساس مجموع زاویه های تعداد مثلث های دورن او است.
مجموع زاویه داخلی: 180 ( n − 2 )
اندازه زاویه داخلی چندضلعی منتظم برابر با تقسیم تعداد ضلع ها است. چون تعداد راس ها با تعداد ضلع ها برابر است.
اندازه هرزاویه داخلی: 180 n ( n − 2 )
مجموع زاویه خارجی هر چندضلعی منتظم برابر با۳۶۰ درجه است. پس برای اندازه گیری زاویه خارجی باید ۳۶۰ درجه به تعداد اضلاع چندضلعی منتظم تقسیم کنیم، تا اندازه زاویه آن مشخص گردد.
مجموع زاویه خارجی:360درجه
اندازه زاویه مجموع زاویه خارجی هر چندضلعی منتظم برابر با۳۶۰ درجه است. پس برای اندازه گیری زاویه خارجی باید ۳۶۰ درجه به تعداد اضلاع چندضلعی منتظم تقسیم کنیم، تا اندازه زاویه آن مشخص گردد.

wiki: زوایای داخلی و خارجی
