در علم آمار، روش های زنجیره مارکف مونت کارلو ( MCMC ) یک کلاس از الگوریتم ها برای نمونه برداری از یک توزیع احتمالی را تشکیل می دهند. با ساخت یک زنجیره مارکف که توزیع مطلوب را به عنوان توزیع تعادل خود دارد، می توان نمونه ای از توزیع مطلوب را با مشاهده زنجیره بعد از چند مرحله بدست آورد. هر چه گام های بیشتری وجود داشته باشد، توزیع نمونه با توزیع مطلوب واقعی مطابقت بیشتری خواهد داشت. معمولاً انتقال از یک گره ی زنجیره به گره ی دیگر با استفاده از روش های قدم زدن تصادفی صورت می گیرد.
معمول ترین کاربرد این الگوریتم ها در محاسبه ی عددی انتگرال های چندگانه است. این انتگرال ها در آمار بیزی، فیزیک محاسباتی، زیست شناسی محاسباتی[ ۱] و زبان شناسی محاسباتی به وجود می آیند. بنابراین می توان گفت زنجیره های مارکف مونت کارلو کاربرد گسترده ای در این زمینه ها دارند. [ ۲]
در آمار بیزی، توسعه اخیر روش های مونت کارلو یک گام کلیدی در محاسبه مدل های سلسله مراتبی بزرگی بوده است که نیازمند ترکیب صدها یا حتی هزاران پارامتر ناشناخته هستند. [ ۳]
در نمونه گیری پدیده های نادر، این الگوریتم ها با تولید نمونه هایی برای پر کردن تدریجی ناحیه ای که نمونه گیری از آن شکست می خورد، مورد استفاده قرار می گیرند. [ ۲]
روش های مونت کارلو نمونه هایی از یک متغیر تصادفی پیوسته ی چند بعدی را با چگالی احتمالِ متناسب با یک تابع شناخته شده ایجاد می کنند. این نمونه ها را می توان برای ارزیابی انتگرال بر روی آن متغیر، به عنوان مقدار پیش بینی شده یا واریانس مورد استفاده قرار داد.
در عمل، معمولاً دسته ای از زنجیره ها که هر کدام از نقطه ای دلخواه ( که معمولاً این نقاط از هم به مقدار کافی فاصله دارند ) ساخته می شوند. این زنجیره ها فرآیندهای تصادفی «قدم زن» هستند که به طور تصادفی با توجه به الگوریتمی که به دنبال مکان هایی با سهم بالا در انتگرال برای حرکت به سمت نقاط بعدی است و به آن ها احتمالات بالاتر اختصاص می دهد، حرکت می کنند. [ ۲]
روش های قدم زدن تصادفی مونت کارلو یک نوع شبیه سازی تصادفی یا روش مونت کارلو هستند. با این حال، در حالی که نمونه های تصادفی به کاررفته در روش های مونت کارلوی معمول به لحاظ آماری مستقل هستند؛ آن هایی که در روش های زنجیره ی مارکف مونت کارلو مورد استفاده قرار می گیرند، خودهمبستگی دارند.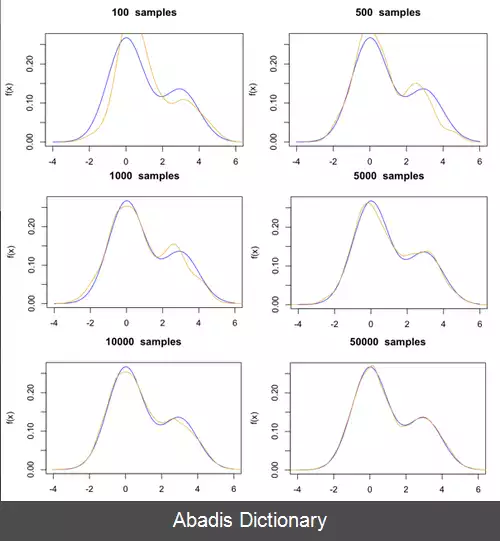
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمعمول ترین کاربرد این الگوریتم ها در محاسبه ی عددی انتگرال های چندگانه است. این انتگرال ها در آمار بیزی، فیزیک محاسباتی، زیست شناسی محاسباتی[ ۱] و زبان شناسی محاسباتی به وجود می آیند. بنابراین می توان گفت زنجیره های مارکف مونت کارلو کاربرد گسترده ای در این زمینه ها دارند. [ ۲]
در آمار بیزی، توسعه اخیر روش های مونت کارلو یک گام کلیدی در محاسبه مدل های سلسله مراتبی بزرگی بوده است که نیازمند ترکیب صدها یا حتی هزاران پارامتر ناشناخته هستند. [ ۳]
در نمونه گیری پدیده های نادر، این الگوریتم ها با تولید نمونه هایی برای پر کردن تدریجی ناحیه ای که نمونه گیری از آن شکست می خورد، مورد استفاده قرار می گیرند. [ ۲]
روش های مونت کارلو نمونه هایی از یک متغیر تصادفی پیوسته ی چند بعدی را با چگالی احتمالِ متناسب با یک تابع شناخته شده ایجاد می کنند. این نمونه ها را می توان برای ارزیابی انتگرال بر روی آن متغیر، به عنوان مقدار پیش بینی شده یا واریانس مورد استفاده قرار داد.
در عمل، معمولاً دسته ای از زنجیره ها که هر کدام از نقطه ای دلخواه ( که معمولاً این نقاط از هم به مقدار کافی فاصله دارند ) ساخته می شوند. این زنجیره ها فرآیندهای تصادفی «قدم زن» هستند که به طور تصادفی با توجه به الگوریتمی که به دنبال مکان هایی با سهم بالا در انتگرال برای حرکت به سمت نقاط بعدی است و به آن ها احتمالات بالاتر اختصاص می دهد، حرکت می کنند. [ ۲]
روش های قدم زدن تصادفی مونت کارلو یک نوع شبیه سازی تصادفی یا روش مونت کارلو هستند. با این حال، در حالی که نمونه های تصادفی به کاررفته در روش های مونت کارلوی معمول به لحاظ آماری مستقل هستند؛ آن هایی که در روش های زنجیره ی مارکف مونت کارلو مورد استفاده قرار می گیرند، خودهمبستگی دارند.

wiki: زنجیره مارکوف مونت کارلو
