رگرسیون لارس یا رگرسیون کمترین زاویه[ الف] یکی از روش های تحلیل رگرسیون است که در آن ضرایب رگرسیون در یک فرایند افزایشی تخمین زده می شوند. [ ۱]
در رگرسیون کمترین زاویه که به آن رگرسیون لارس هم گفته می شود، ضرایب رگرسیون در یک فرایند افزایشی به شکل زیر تخمین زده می شوند:[ ۱]
• در ابتدا تمام ضرایب β i {\displaystyle \beta _{i}} با عدد صفر مقداردهی می شوند.
• متغیر مستقل x j {\displaystyle x_{j}} که بیشترین ضریب همبستگی را با متغیر وابسته y {\displaystyle y} دارد انتخاب می شود.
• β j {\displaystyle \beta _{j}} در جهت علامت ضریب همبستگی افزایش می یابد تا جایی که همبستگی متغیر دیگری مانند x k {\displaystyle x_{k}} با مانده r = y − y ^ {\displaystyle r=y - {\hat {y}}} از همبستگی x j {\displaystyle x_{j}} با مانده فزونی بیابد.
• حال ( β j {\displaystyle \beta _{j}} , β k {\displaystyle \beta _{k}} ) در جهت بردار بهینه ای که از کمترین مربعاتِ ( x j {\displaystyle x_{j}} , x k {\displaystyle x_{k}} ) به دست آمده افزایش داده می شود و همزمان مانده ها نیز محاسبه می شوند. متغیر دیگری پیدا می شود که همبستگی بیشتری با مانده متغیرهایی که تا به حال انتخاب شده اند داشته باشد، و به جمع متغیرهایی انتخاب شده اضافه می شود و این روند تا انتخاب تمام متغیرها ادامه خواهد یافت.
رگرسیون لارس مانند رگرسیون لَسو باعث می شوند مدل نهائی خلوت شود و بسیاری از ضرایبِ مدل صفر شود. این مدل برای داده هایی بُعد بالا مورد استفاده قرار می گیرد. [ ۲]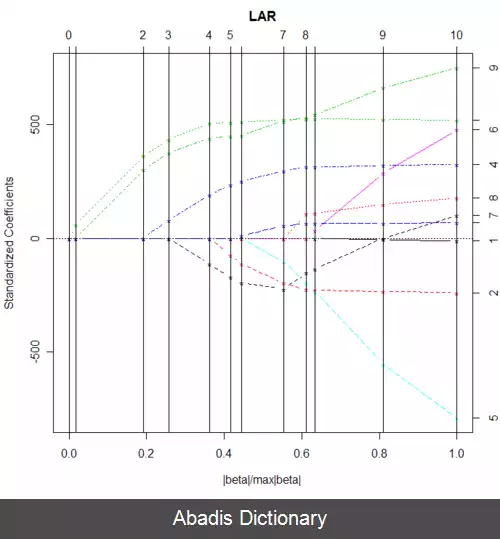
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر رگرسیون کمترین زاویه که به آن رگرسیون لارس هم گفته می شود، ضرایب رگرسیون در یک فرایند افزایشی به شکل زیر تخمین زده می شوند:[ ۱]
• در ابتدا تمام ضرایب β i {\displaystyle \beta _{i}} با عدد صفر مقداردهی می شوند.
• متغیر مستقل x j {\displaystyle x_{j}} که بیشترین ضریب همبستگی را با متغیر وابسته y {\displaystyle y} دارد انتخاب می شود.
• β j {\displaystyle \beta _{j}} در جهت علامت ضریب همبستگی افزایش می یابد تا جایی که همبستگی متغیر دیگری مانند x k {\displaystyle x_{k}} با مانده r = y − y ^ {\displaystyle r=y - {\hat {y}}} از همبستگی x j {\displaystyle x_{j}} با مانده فزونی بیابد.
• حال ( β j {\displaystyle \beta _{j}} , β k {\displaystyle \beta _{k}} ) در جهت بردار بهینه ای که از کمترین مربعاتِ ( x j {\displaystyle x_{j}} , x k {\displaystyle x_{k}} ) به دست آمده افزایش داده می شود و همزمان مانده ها نیز محاسبه می شوند. متغیر دیگری پیدا می شود که همبستگی بیشتری با مانده متغیرهایی که تا به حال انتخاب شده اند داشته باشد، و به جمع متغیرهایی انتخاب شده اضافه می شود و این روند تا انتخاب تمام متغیرها ادامه خواهد یافت.
رگرسیون لارس مانند رگرسیون لَسو باعث می شوند مدل نهائی خلوت شود و بسیاری از ضرایبِ مدل صفر شود. این مدل برای داده هایی بُعد بالا مورد استفاده قرار می گیرد. [ ۲]

wiki: رگرسیون لارس
