رگرسیون ریج ( به انگلیسی: Ridge regression ) یکی از نسخه های رگرسیون خطی است که در مسائلی با متغیرهای مستقل دارای همبستگی بالا برای تخمین ضرایب استفاده می شود و مشکل هم خطی چندگانه را کاهش می دهد. ریج، همچنین یکی از روش های تنظیم مدل است که از بیش برازش در رگرسیون جلوگیری می کند. در این روش، نُرمِ L 2 ضرایب به تابع هزینه مجموع مربعات خطا[ الف] حین فرایند آموزش مدل، افزوده می شود. با این کار وزن های مدل تا حد امکان کوچک نگه داشته می شوند. [ ۱]
فرض کنید در مسئله رگرسیون، مجموعه داده ها شامل N جفت متغیر پیشگو و متغیر پاسخ به صورت D = { ( x 1 , y 1 ) , ⋯ , ( x N , y N ) } باشد. هدف بدست آوردن y به عنوان ترکیبی خطی از x است یعنی x T β + β 0 . رگرسیون خطی معمولی به شکل زیر در پی یافتن و بهینه است به طوری که مجموع مربعات خطا را کمینه کند:
min β 0 , β { ∑ i = 1 N ( y i − β 0 − x i T β ) 2 }
در رگرسیون ریج ضریبی از نُرمِ L 2 به تابع هزینه اضافه می شود:
min β ∈ R p { ‖ Y − X β ‖ 2 2 + λ ‖ β ‖ 2 2 }
پارامتر λ میزان جریمه روی نُرمِ L 2 را مشخص می کند. اضافه کردن ضریبی از نُرمِ L 2 به تابع هزینه معادلِ ایجاد محدودیتی بر روی نُرمِ L 2 است:
min β ∈ R p { ‖ Y − X β ‖ 2 2 } subject to ‖ β ‖ 2 2 ≤ t 2
که منظور از ‖ v ‖ p در واقع، نُرمِ ℓ p است که به صورت زیر محاسبه می شود:
بنابراین، رگرسیون ریج محدودیت های بیشتری را روی ضرایب مدل اعمال می کند. چراکه در این روش افزون بر تلاش برای کمینه کردن میانگین خطای مربعات خطاها، جریمه ای[ ب] روی ضرایب هم در نظر گرفته می شود. در نتیجه ترجیح بر انتخاب ضرایبی با اندازهٔ کوچک یا نزدیک به صفر است تا جملهٔ جدید افزوده شده به تابع هزینه نیز کوچک شود[ ۲]
برای به دست آوردن فرم بستهٔ جواب به فرم ماتریسی تابع هزینه را توجه کنید:
( Y − X β ) T ( Y − X β ) + λ β T β
کافیست نسبت به β مشتق بگیریم:
X T Y = ( X T X + λ I ) β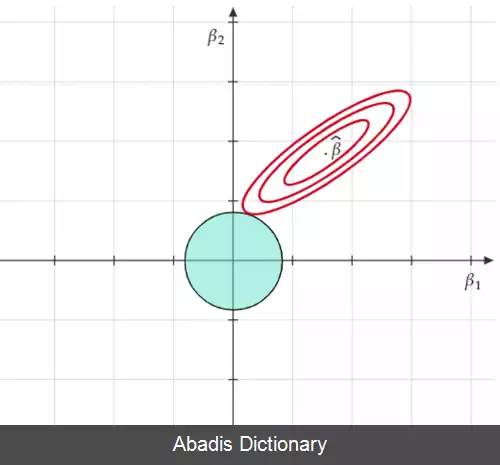
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنید در مسئله رگرسیون، مجموعه داده ها شامل N جفت متغیر پیشگو و متغیر پاسخ به صورت D = { ( x 1 , y 1 ) , ⋯ , ( x N , y N ) } باشد. هدف بدست آوردن y به عنوان ترکیبی خطی از x است یعنی x T β + β 0 . رگرسیون خطی معمولی به شکل زیر در پی یافتن و بهینه است به طوری که مجموع مربعات خطا را کمینه کند:
min β 0 , β { ∑ i = 1 N ( y i − β 0 − x i T β ) 2 }
در رگرسیون ریج ضریبی از نُرمِ L 2 به تابع هزینه اضافه می شود:
min β ∈ R p { ‖ Y − X β ‖ 2 2 + λ ‖ β ‖ 2 2 }
پارامتر λ میزان جریمه روی نُرمِ L 2 را مشخص می کند. اضافه کردن ضریبی از نُرمِ L 2 به تابع هزینه معادلِ ایجاد محدودیتی بر روی نُرمِ L 2 است:
min β ∈ R p { ‖ Y − X β ‖ 2 2 } subject to ‖ β ‖ 2 2 ≤ t 2
که منظور از ‖ v ‖ p در واقع، نُرمِ ℓ p است که به صورت زیر محاسبه می شود:
بنابراین، رگرسیون ریج محدودیت های بیشتری را روی ضرایب مدل اعمال می کند. چراکه در این روش افزون بر تلاش برای کمینه کردن میانگین خطای مربعات خطاها، جریمه ای[ ب] روی ضرایب هم در نظر گرفته می شود. در نتیجه ترجیح بر انتخاب ضرایبی با اندازهٔ کوچک یا نزدیک به صفر است تا جملهٔ جدید افزوده شده به تابع هزینه نیز کوچک شود[ ۲]
برای به دست آوردن فرم بستهٔ جواب به فرم ماتریسی تابع هزینه را توجه کنید:
( Y − X β ) T ( Y − X β ) + λ β T β
کافیست نسبت به β مشتق بگیریم:
X T Y = ( X T X + λ I ) β

wiki: رگرسیون ریج
