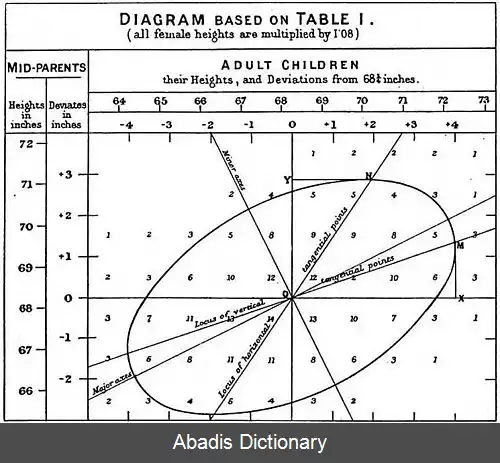
رگرسیون خطی یا تنازل خطی یا وایازی خطی[ الف] یکی از روش های تحلیل رگرسیون است. رگرسیون یک نوع مدل آماری ست برای پیش بینی یک متغیر از روی یک یا چند متغیر دیگر. رگرسیون خطی نوعی تابع پیش بینی کننده خطی است که در آن متغیر وابسته — متغیری که قرار است پیش بینی شود — به صورت ترکیبی خطی از متغیرهای مستقل پیش بینی می شود، بدین معنی که هر کدام از متغیرهای مستقل در ضریبی که در فرایند تخمین برای آن متغیر به دست آمده ضرب می شود؛ جواب نهائی مجموع حاصل ضرب ها به علاوه یک مقدار ثابت خواهد بود که آن هم در فرایند تخمین به دست آمده است. ساده ترین نوع رگرسیون خطی، رگرسیون خطی ساده است که برخلاف رگرسیون خطی چندگانه، تنها یک متغیر مستقل دارد. نوع دیگر رگرسیون خطی رگرسیون خطی چندمتغیره است که در آن به جای پیش بینی یک متغیر وابسته چندین متغیر وابسته پیش بینی می شود.
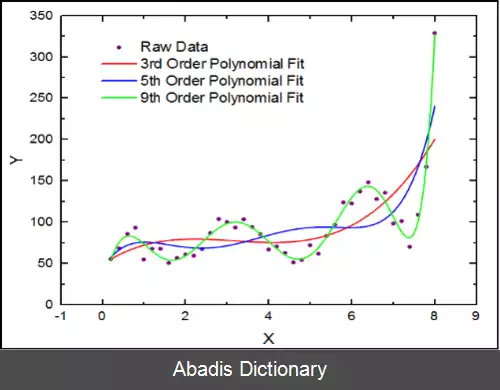
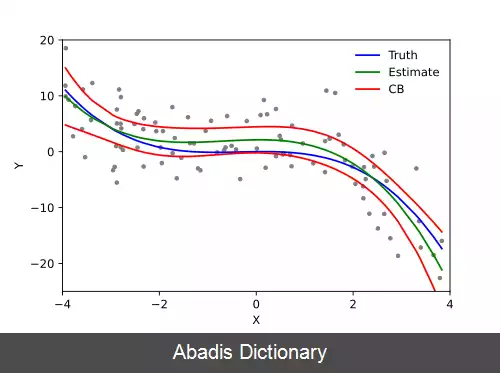
فرایند تخمین سعی می کند ضرایبِ مدل رگرسیون خطی را به گونه ای انتخاب کند که با داده های موجود همخوانی داشته باشد، یعنی پیش بینی ها به مقادیر رؤیت شده در داده ها نزدیک باشند و یکی از مهم ترین مسائل در رگرسیون خطی، به حداقل رساندن اختلاف بین این دو است. راه های مختلفی برای حل این مسئله وجود دارد. در روش های احتمالی، مدل های رگرسیون خطی سعی در برآورد توزیع احتمال شرطیِ متغیر وابسته ( و نه توزیع احتمال توأم ) دارند که از آن طریق آماره ای از متغیر وابسته را به عنوان پیش بینی نهایی به کار می برند. از متداول ترین آماره های مورد استفاده میانگین است، اگر چه سایر آماره ها نظیر میانه یا چندک ها نیز مورد استفاده قرار می گیرند.
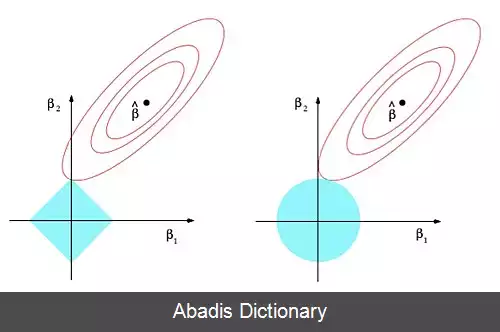
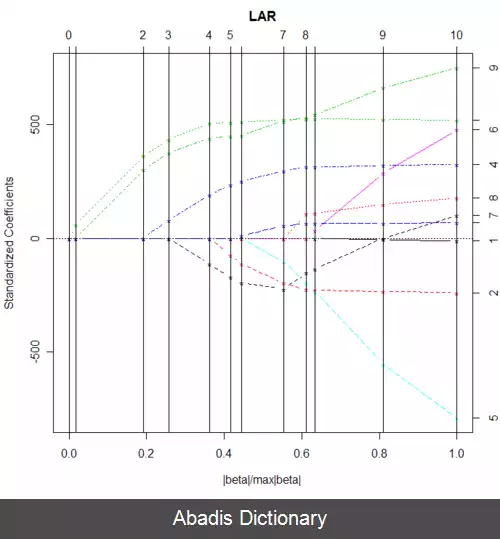
یکی دیگر از روش های متداول تخمین، روش کمترین مربعات است که در آن مجموع مربع تفاضل پیش بینی ها و داده های وابسته کمینه می شود. این روش مستلزم پیدا کردن وارونه ضرب خارجی ماتریس تمام داده های مستقل با ماتریس ترانهادهٔ آن است، فرآیندی که می تواند به علت وارونه ناپذیری ماتریس نهائی و کمبود داده پرهزینه و ناکارا باشد. از این رو عموماً از روش های جایگزین مانند گرادیان کاهشی تصادفی استفاده می شود. با اینکه روش کمترین مربعات از متداول ترین روش های تخمین مدل رگرسیون خطی است اما روش های دیگری مانند کمترین قدرمطلق ها ( که در آن مجموع قدرمطلق تفاضل پیش بینی و داده وابسته به عنوان تابع هزینه در نظرگرفته می شود ) یا تخمین جریمه یافتهٔ کمترین مربعات ( مانند جریمهٔ نُرمِ L 2 و جریمهٔ نُرمِ L 1 ) نیز مورد استفاده قرار می گیرد.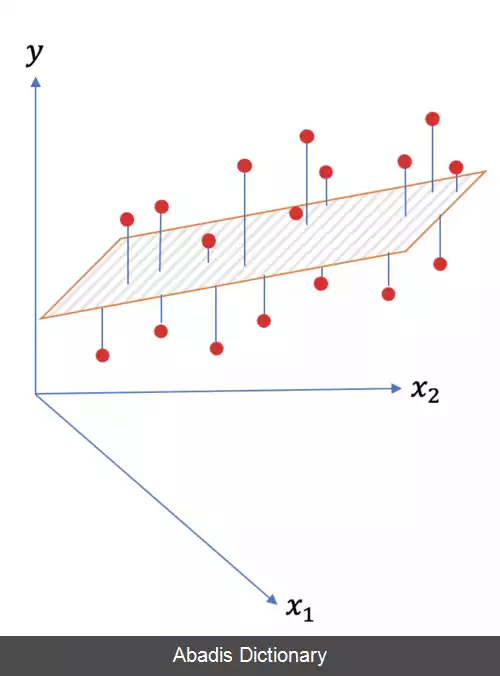
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرایند تخمین سعی می کند ضرایبِ مدل رگرسیون خطی را به گونه ای انتخاب کند که با داده های موجود همخوانی داشته باشد، یعنی پیش بینی ها به مقادیر رؤیت شده در داده ها نزدیک باشند و یکی از مهم ترین مسائل در رگرسیون خطی، به حداقل رساندن اختلاف بین این دو است. راه های مختلفی برای حل این مسئله وجود دارد. در روش های احتمالی، مدل های رگرسیون خطی سعی در برآورد توزیع احتمال شرطیِ متغیر وابسته ( و نه توزیع احتمال توأم ) دارند که از آن طریق آماره ای از متغیر وابسته را به عنوان پیش بینی نهایی به کار می برند. از متداول ترین آماره های مورد استفاده میانگین است، اگر چه سایر آماره ها نظیر میانه یا چندک ها نیز مورد استفاده قرار می گیرند.
یکی دیگر از روش های متداول تخمین، روش کمترین مربعات است که در آن مجموع مربع تفاضل پیش بینی ها و داده های وابسته کمینه می شود. این روش مستلزم پیدا کردن وارونه ضرب خارجی ماتریس تمام داده های مستقل با ماتریس ترانهادهٔ آن است، فرآیندی که می تواند به علت وارونه ناپذیری ماتریس نهائی و کمبود داده پرهزینه و ناکارا باشد. از این رو عموماً از روش های جایگزین مانند گرادیان کاهشی تصادفی استفاده می شود. با اینکه روش کمترین مربعات از متداول ترین روش های تخمین مدل رگرسیون خطی است اما روش های دیگری مانند کمترین قدرمطلق ها ( که در آن مجموع قدرمطلق تفاضل پیش بینی و داده وابسته به عنوان تابع هزینه در نظرگرفته می شود ) یا تخمین جریمه یافتهٔ کمترین مربعات ( مانند جریمهٔ نُرمِ L 2 و جریمهٔ نُرمِ L 1 ) نیز مورد استفاده قرار می گیرد.






wiki: رگرسیون خطی
