رویه مربعی

در هندسهٔ تحلیلی، رویه های درجهٔ دوم در فضای سه بعدی دسته ای از رویه ها هستند که به این صورت تعریف می شوند: مکان هندسی همهٔ نقاطی مانند P = ( x , y , z ) که در معادلهٔ F ( x , y , z ) = 0 صدق کنند که F یک تابع درجهٔ دو است. [ ۱]
به عنوان مثال کُره یک رویهٔ درجه دو است؛ زیرا معادلهٔ استاندارد کره یک معادلهٔ درجه دو است: x 2 + y 2 + z 2 = r 2
به طور کلّی تر، ابررویه های درجه دو در فضای R n دسته ای از ابررویه های n − 1 - بعدی هستند که به این صورت تعریف می شوند: مجموعهٔ همهٔ نقاطی مانند P = ( x 1 , x 2 , … , x n ) که در معادلهٔ F ( x 1 , x 2 , … , x n ) = 0 صدق کنند که F یک تابع درجهٔ دو است.
در نتیجه می توان مقاطع مخروطی را حالت خاصی از رویه های درجه دو ( حالت n = 2 ) دانست. البتّه در فضای دوبعدی به جای «رویه» باید از اصطلاح «خم» استفاده کرد.
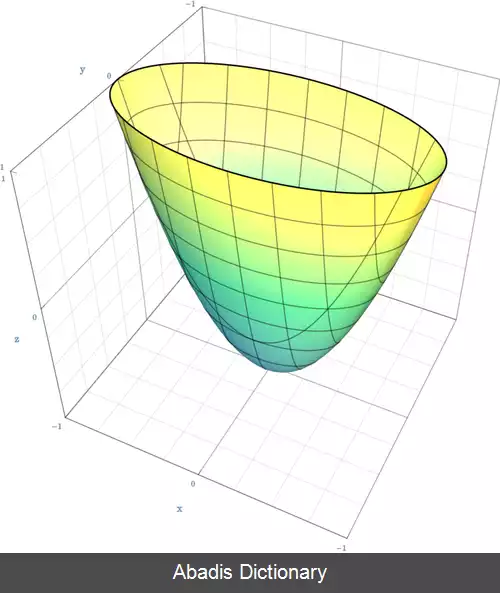
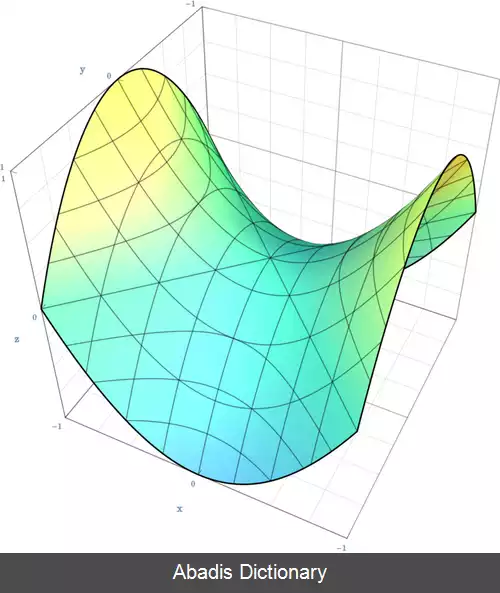
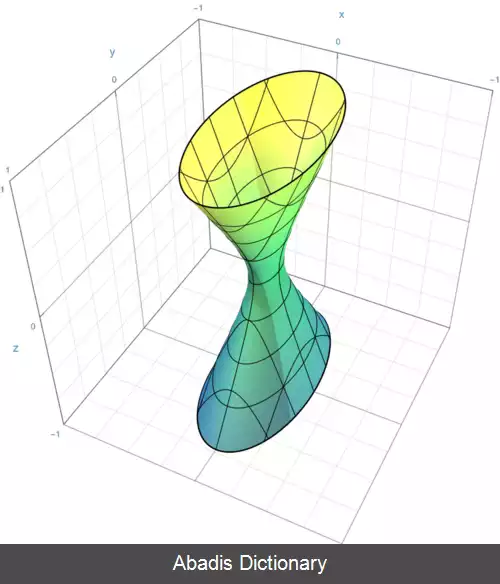
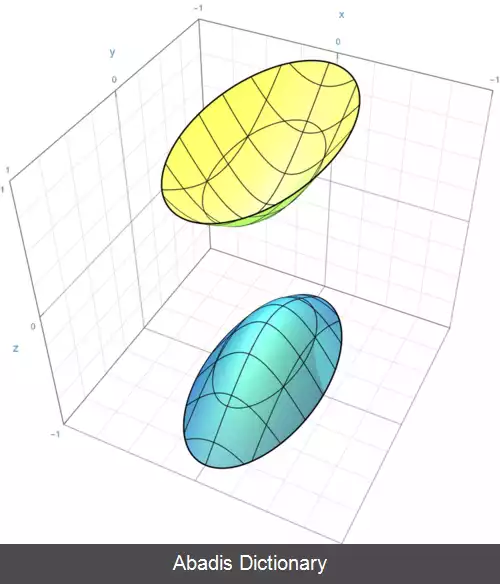
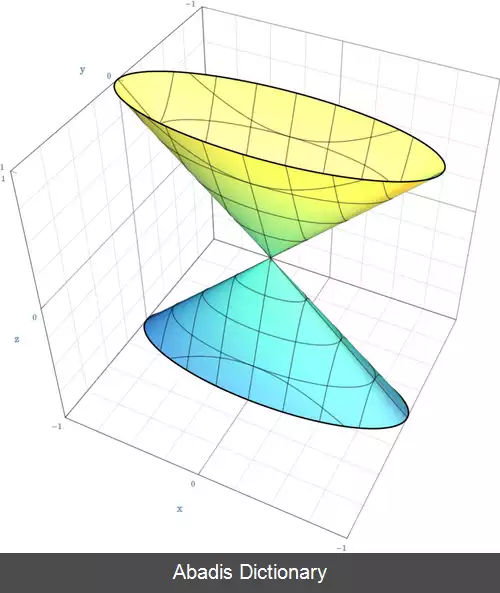
در فضای سه بعدی، رویه های درجه دو به شاخه های زیر تقسیم می شود:[ ۱]
وقتی که دو یا هر سه ثابت ( a و b و c ) با یکدیگر برابر باشند، رویهٔ درجه دو دورانی به دست می آید: