روش گروه جفتی وزن دار با میانگین حسابی ( به انگلیسی: Weighted Pair Group Method with Arithmetic Mean ( WPGMA ) ) یک متد ساده خوشه بندی سلسله مراتبی تجمعی ( از پایین به بالا ) می باشد که هدف آن، ایجاد یک درخت ریشه دار ( که به آن دندروگرام می گویند ) می باشد که ساختار موجود در یک ماتریس زوج فاصله را نشان می دهد. [ ۱] این متد را به رابرت آر. سوکال و چارلز دانکن میشنر نسبت می دهند.
متد جفت گروه وزن دار با میانگین حسابی، شبیه به نوع بی وزن آن، یعنی متد جفت گروه بدون وزن با میانگین حسابی است که به طور عمده بر مبنای توده کردن داده ها یا خوشه بندی سلسله مراتبی مخصوصاً برای ساخت درخت فیلوژنتیک در بیوانفورماتیک به کار می رود. [ ۲]
همان طور که در ابتدای کار ذکر شد، الگوریتم جفت گروه وزن دار با میانگین حسابی، با استفاده از یک درخت ریشه دار به نام دندوگرام، ساختار موجود در یک ماتریس زوج فاصله را نشان می دهد. اگر این ماتریس، یک ماتریس n ∗ n باشد، این الگوریتم شامل n − 1 گام می باشد؛ در هر گام، نزدیک ترین دو خوشه، در اینجا فرض کنید a i و a j ، به یک خوشه سطح بالاتر ترکیب می شوند. سپس فاصلهٔ آن با یک خوشهٔ دیگر فرضی به نام a l ، از طریق میانگین حسابی فاصلهٔ بین a i ، a l و a j ، a l حساب می شود:[ ۱]
D i s t ( a i ∪ a j ) , a k = D i s t a i , a k + D i s t a j , a k 2
اگر فرض کنیم متد جفت گروه وزن دار با میانگین حسابی، روی یک ماتریس n ∗ n کار می کند، در نتیجه شامل n − 1 گام می باشد که در مثال زیر، یک ماتریس ۴ * ۴ داده شده، بررسی می شود.
فرض کنید ۴ المان ( a 1 , a 2 , a 3 , a 4 ) داریم و ماتریس زیر به نام Dist ( مخفف فاصله ) که نشان دهندهٔ فاصلهٔ بین هردو المان را نشان می دهد و همچنین ϕ نشان دهندهٔ فاصلهٔ بین ۲ گره در درخت دندوگرام باشد:
در این جدول، کوتاه ترین فاصله بین ۲ المان مختلف, متعلق بین a 1 و a 2 و برابر با ۱۵ می باشد ( D i s t ( a 1 , a 2 ) = 15 ) .
حال فرض کنید گره ای که a 1 و a 2 را به هم متصل می کند، c 1 نام دارد. در نتیجه به درخت دندوگرام، گره c 1 را اضافه می کنیم که فاصله این گره با a 1 و a 2 از راه زیر محاسبه می شود: ϕ ( a 1 , c 1 ) = ϕ ( a 2 , c 1 ) = D i s t ( a 1 , a 2 ) / 2 = 7. 5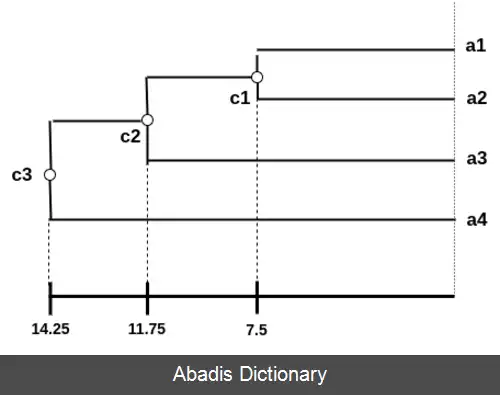
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمتد جفت گروه وزن دار با میانگین حسابی، شبیه به نوع بی وزن آن، یعنی متد جفت گروه بدون وزن با میانگین حسابی است که به طور عمده بر مبنای توده کردن داده ها یا خوشه بندی سلسله مراتبی مخصوصاً برای ساخت درخت فیلوژنتیک در بیوانفورماتیک به کار می رود. [ ۲]
همان طور که در ابتدای کار ذکر شد، الگوریتم جفت گروه وزن دار با میانگین حسابی، با استفاده از یک درخت ریشه دار به نام دندوگرام، ساختار موجود در یک ماتریس زوج فاصله را نشان می دهد. اگر این ماتریس، یک ماتریس n ∗ n باشد، این الگوریتم شامل n − 1 گام می باشد؛ در هر گام، نزدیک ترین دو خوشه، در اینجا فرض کنید a i و a j ، به یک خوشه سطح بالاتر ترکیب می شوند. سپس فاصلهٔ آن با یک خوشهٔ دیگر فرضی به نام a l ، از طریق میانگین حسابی فاصلهٔ بین a i ، a l و a j ، a l حساب می شود:[ ۱]
D i s t ( a i ∪ a j ) , a k = D i s t a i , a k + D i s t a j , a k 2
اگر فرض کنیم متد جفت گروه وزن دار با میانگین حسابی، روی یک ماتریس n ∗ n کار می کند، در نتیجه شامل n − 1 گام می باشد که در مثال زیر، یک ماتریس ۴ * ۴ داده شده، بررسی می شود.
فرض کنید ۴ المان ( a 1 , a 2 , a 3 , a 4 ) داریم و ماتریس زیر به نام Dist ( مخفف فاصله ) که نشان دهندهٔ فاصلهٔ بین هردو المان را نشان می دهد و همچنین ϕ نشان دهندهٔ فاصلهٔ بین ۲ گره در درخت دندوگرام باشد:
در این جدول، کوتاه ترین فاصله بین ۲ المان مختلف, متعلق بین a 1 و a 2 و برابر با ۱۵ می باشد ( D i s t ( a 1 , a 2 ) = 15 ) .
حال فرض کنید گره ای که a 1 و a 2 را به هم متصل می کند، c 1 نام دارد. در نتیجه به درخت دندوگرام، گره c 1 را اضافه می کنیم که فاصله این گره با a 1 و a 2 از راه زیر محاسبه می شود: ϕ ( a 1 , c 1 ) = ϕ ( a 2 , c 1 ) = D i s t ( a 1 , a 2 ) / 2 = 7. 5

