روش پَس گرد ( به انگلیسی: Backtracking ) یکی از شیوه های کلی جستجوی فضای حالت برای حل مسائل ترکیبیاتی است. این شیوه، تمام ترکیب های ممکن را بررسی می کند تا یک جواب پیدا کند یا تمام جواب های ممکن را شمارش کند. تنها مزیت روش پسگرد در این است که می توان حالت هایی را بدون آنکه صریحاً بررسی شوند، با در نظر گرفتن ویژگی های مسئله، کنار گذاشت. واژهٔ BackTrack به وسیلهٔ یک ریاضی دان آمریکایی به نام D. H. lehmer در سال ۱۹۵۰ ابداع شد.
در بسیاری از مسائل می توان بدون نیاز به بررسی تمام ترکیبات، از اینکه جواب مسئله توسط چه ترکیبی از مقادیر قابل تحقق نیست اطمینان بدست آورد و بدین ترتیب بخش های بزرگی از فضای جستجو را کنار گذاشت. اگر حل مسئله با انتساب مقادیر به n متغیر محقق شود، در بسیار مسائل با توجه به ویژگی های مسئله، می توان پیش از کامل شدن انتساب مقادیر، از اینکه انتساب جزئی برای رسیدن به جواب، «امیدبخش» نیست اطمینان بدست آورد و از این طریق از بررسی حالت هایی که از توسعه این انتساب به دست می آیند صرفنظر کرد.
روش پس گرد شیوه ای در حل مسائل است که از علامت های خاصی برای بیان اینکه راه حل کاندیدی به حل مسئله می انجامد یا خیر استفاده می کند. این رویکرد برای حل مسائل درخت فضای آن مسئله را ایجاد کرده و تعیین می کند کدام گره امید بخش است. الگوریتم های عقب گردی از تابلوها یا علامت هایی برای بیان اینکه یک راه حل کاندید به حل مسئله نمی انجامد استفاده می کند. عقبگرد، حالت اصلاح شدهٔ جستجوی عمقی یک درخت می باشد. [ ۱]
مثال اول در روش پس گرد مسئله قفل رمزی می باشد. یک قفل رمزی شامل n کلید دیجیتالی است که هر کلید فقط دو حالت بسته ( ۱ ) یا حالت باز ( ۰ ) دارد. می دانیم که n کلید دیجیتالی تعداد 2nحالت مختلف را پدیدمی آورند و این قفل تنها با یک حالت که همان رمز است باز می شود.
مثال دوم در روش پس گرد مسئله چند وزیر می باشد. هدف این مسئله چیدن n وزیر در یک صفحه شطرنج n*n است به گونه ای که هیچ دو وزیری یکدیگر را تهدید نکنند.
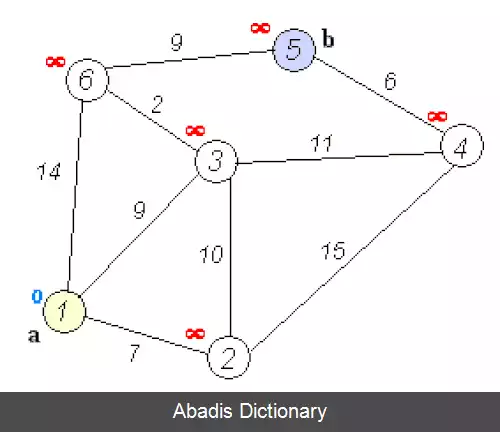
مثال سوم در حل مسئله رنگ آمیزی گراف می باشد. در این مسئله می خواهیم تمام راه های ممکن جهت رنگ آمیزی گره های یک گراف بدون جهت را با استفاده از حداکثر m رنگ متفاوت پیدا کنیم، به گونه ای که هیچ دو رأس مجاوری هم رنگ نباشند.
مثال چهارم مسئله حاصل جمع زیر مجموعه ها می باشد. در این مسئله، n عدد صحیح مثبت wi و یک عدد صحیح مثبت w داریم. هدف پیدا کردن تمامی زیر مجموعه هایی از این اعداد صحیح می باشد که حاصل جمع آن ها بربر w است.

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر بسیاری از مسائل می توان بدون نیاز به بررسی تمام ترکیبات، از اینکه جواب مسئله توسط چه ترکیبی از مقادیر قابل تحقق نیست اطمینان بدست آورد و بدین ترتیب بخش های بزرگی از فضای جستجو را کنار گذاشت. اگر حل مسئله با انتساب مقادیر به n متغیر محقق شود، در بسیار مسائل با توجه به ویژگی های مسئله، می توان پیش از کامل شدن انتساب مقادیر، از اینکه انتساب جزئی برای رسیدن به جواب، «امیدبخش» نیست اطمینان بدست آورد و از این طریق از بررسی حالت هایی که از توسعه این انتساب به دست می آیند صرفنظر کرد.
روش پس گرد شیوه ای در حل مسائل است که از علامت های خاصی برای بیان اینکه راه حل کاندیدی به حل مسئله می انجامد یا خیر استفاده می کند. این رویکرد برای حل مسائل درخت فضای آن مسئله را ایجاد کرده و تعیین می کند کدام گره امید بخش است. الگوریتم های عقب گردی از تابلوها یا علامت هایی برای بیان اینکه یک راه حل کاندید به حل مسئله نمی انجامد استفاده می کند. عقبگرد، حالت اصلاح شدهٔ جستجوی عمقی یک درخت می باشد. [ ۱]
مثال اول در روش پس گرد مسئله قفل رمزی می باشد. یک قفل رمزی شامل n کلید دیجیتالی است که هر کلید فقط دو حالت بسته ( ۱ ) یا حالت باز ( ۰ ) دارد. می دانیم که n کلید دیجیتالی تعداد 2nحالت مختلف را پدیدمی آورند و این قفل تنها با یک حالت که همان رمز است باز می شود.
مثال دوم در روش پس گرد مسئله چند وزیر می باشد. هدف این مسئله چیدن n وزیر در یک صفحه شطرنج n*n است به گونه ای که هیچ دو وزیری یکدیگر را تهدید نکنند.
مثال سوم در حل مسئله رنگ آمیزی گراف می باشد. در این مسئله می خواهیم تمام راه های ممکن جهت رنگ آمیزی گره های یک گراف بدون جهت را با استفاده از حداکثر m رنگ متفاوت پیدا کنیم، به گونه ای که هیچ دو رأس مجاوری هم رنگ نباشند.
مثال چهارم مسئله حاصل جمع زیر مجموعه ها می باشد. در این مسئله، n عدد صحیح مثبت wi و یک عدد صحیح مثبت w داریم. هدف پیدا کردن تمامی زیر مجموعه هایی از این اعداد صحیح می باشد که حاصل جمع آن ها بربر w است.





wiki: روش پس گرد
