روش نلدر - مید یا روش سیمپلکس سراشیبی، یک روش عددی رایج در پیدا کردن کمینه یا بیشینه یک تابع هدف در فضای بهینه سازی چند بعدی می باشد. این روش از مرتبه صفر بوده و بنابراین در مسائل بهینه سازی غیرخطی که در آنها به دست آوردن مشتق تابع ناممکن یا مشکل باشد، قابل پیاده سازی است. با این وجود، روش نلدر - مید یک روش ابتکاری است که می تواند به نقاط غیرایستا همگرا شود. [ ۱]
روش نلدر - مبد در سال ۱۹۶۵ و توسط جان نلدر و راگر مید ارائه شده است. [ ۲]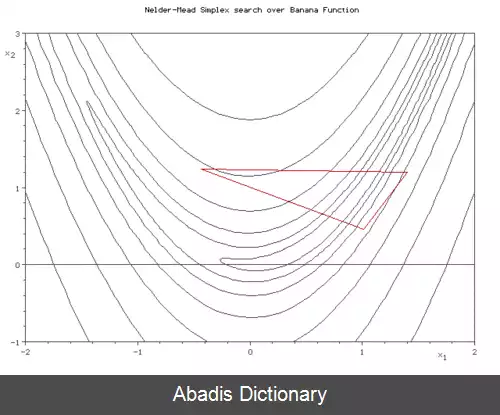
روش نلدر - مبد در سال ۱۹۶۵ و توسط جان نلدر و راگر مید ارائه شده است. [ ۲]


wiki: روش نلدر مید
روش نلدر - مید ( به انگلیسی: Nelder - Mead method ) یا روش سیمپلکس سراشیبی، یک روش عددی رایج در پیدا کردن کمینه یا بیشینه یک تابع هدف در فضای بهینه سازی چند بعدی می باشد. این یک روش جستجوی مستقیم ( بر اساس مقایسه عملکرد ) است و اغلب برای مشکلات بهینه سازی غیرخطی است که مشتقات آن ممکن است مشخص نباشد، استفاده می شود. با این حال، تکنیک Nelder - Mead یک روش جستجوی اکتشافی است که می تواند به نقاط غیر ثابت، [ ۱] در مورد مسائلی که می توان با روشهای جایگزین حل گردد، همگرا شود. [ ۲]
روش نلدر - مید توسط جان نلدر و راجر مید در سال ۱۹۶۵ پیشنهاد شد، [ ۳] که به عنوان توسعه ای از روش Spendley و همکاران بود. [ ۴]
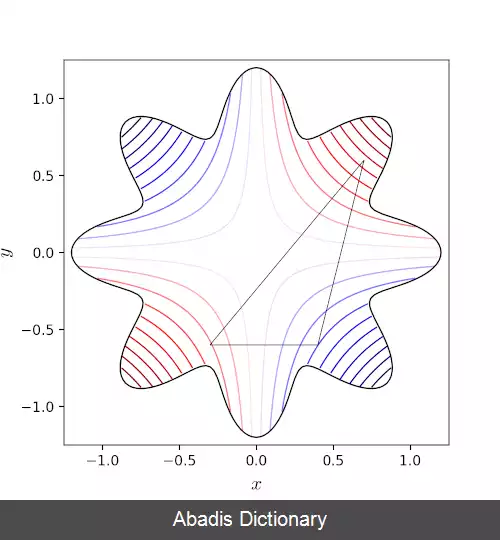
در این روش از مفهوم سیمپلکس استفاده شده است، که یک چندبر ویژه با n+1 راس در یک n بعدی می باشد. نمونه هایی از سیمپلکس ها عبارتند از: یک پاره خط بر روی یک خط، یک مثلث در صفحه، یک چهار وجهی در فضای سه بعدی و غیره.
هنگامی که تابع هدف به نرمی تغییر می کند و یکتا می باشد، این روش یک بهینه سازی محلی برای یک مسئله با n متغیر را تقریب می کند. پیاده سازی های معمولی توابع را به حداقل می رسانند، یا با به کمینه کردن − f ( x ) ، f ( x ) را بیشینه می کنند.
به عنوان مثال، در یک پل تعلیق مهندس باید انتخاب کند که هر بند، کابل و اسکله چقدر ضخیم باشد. این عناصر به هم وابسته هستند، اما تجسم تأثیر تغییر هر عنصر خاص کار ساده ای نیست. شبیه سازی چنین ساختارهای پیچیده ای از لحاظ محاسباتی اغلب پر هزینه بوده و احتمالاً ساعت ها برای اجرای آن طول می کشد. روش Nelder - Mead، در نوع اصلی نیاز به بیش از دو ارزیابی در هر تکرار ندارد، به جز عملیات منقبض شدن که در ادامه شرح داده شده است، که در مقایسه با برخی دیگر از روش های بهینه سازی جستجوی مستقیم، مورد توجه است. با این حال، مجموع تعداد تکرارها، ممکن است از حد مطلوب پیشنهادی بیشتر باشد.
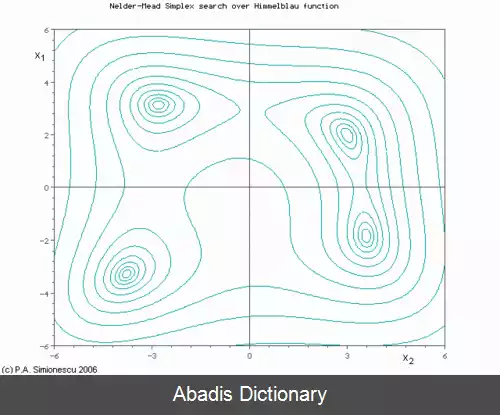
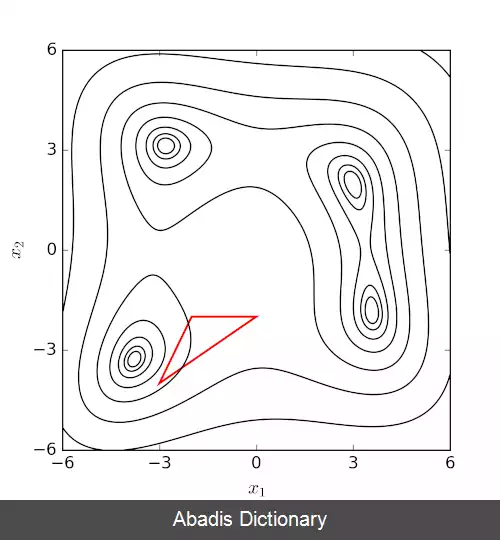
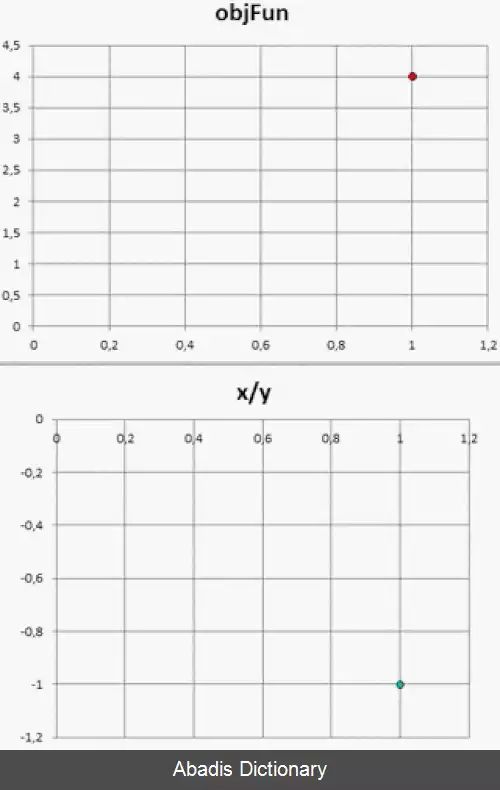
روش نلدر – مید در یک مسئله n بعدی، مجموعه از n+1 نقطه آزمایشی که به صورت سیمپلکس است را در نظر می گیرد. سپس به منظور پیدا کردن یک نقطه آزمایشی جدید و جایگزینی یکی از نقاط آزمایشی قدیمی با مورد جدید، رفتا تابع مورد نظر در هر نقطه آزمایشی، مورد بررسی قرار می گیرد و سپس این روش ادمه پیدا می کند. ساده ترین رویکرد جایگزینی بدترین نقطه، از لحاظ مقدار، با یک نقطه منعکس شده، از طریق مرکز n نقطه باقی مانده می باشد. اگر این نقطه منعکس شده بهتر از نقطه فعلی باشد، می توانیم کشیدگی را در امتداد این خط امتحان کنیم. از طرفی دیگر، اگر این نکته جدید بهتر از مقدار نقطه قبلی نباشد، در واقع ما در یک دره قدم می گذاریم، بنابراین سیمپلکس را در جهت بدست آوردن یک نقطه بهتر منقبض می کنیم. توضیح شهودی الگوریتم از "دستور العمل های عددی":[ ۵]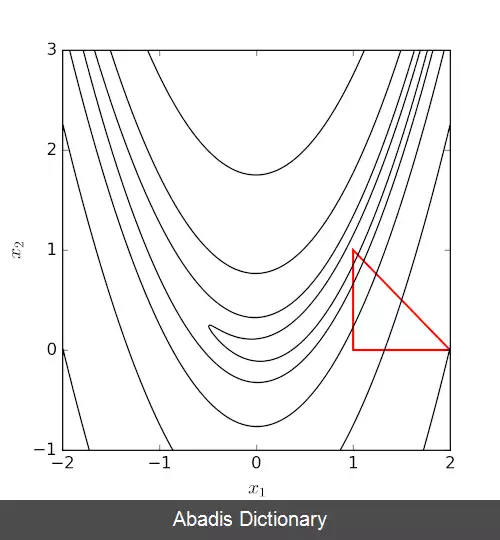
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفروش نلدر - مید توسط جان نلدر و راجر مید در سال ۱۹۶۵ پیشنهاد شد، [ ۳] که به عنوان توسعه ای از روش Spendley و همکاران بود. [ ۴]
در این روش از مفهوم سیمپلکس استفاده شده است، که یک چندبر ویژه با n+1 راس در یک n بعدی می باشد. نمونه هایی از سیمپلکس ها عبارتند از: یک پاره خط بر روی یک خط، یک مثلث در صفحه، یک چهار وجهی در فضای سه بعدی و غیره.
هنگامی که تابع هدف به نرمی تغییر می کند و یکتا می باشد، این روش یک بهینه سازی محلی برای یک مسئله با n متغیر را تقریب می کند. پیاده سازی های معمولی توابع را به حداقل می رسانند، یا با به کمینه کردن − f ( x ) ، f ( x ) را بیشینه می کنند.
به عنوان مثال، در یک پل تعلیق مهندس باید انتخاب کند که هر بند، کابل و اسکله چقدر ضخیم باشد. این عناصر به هم وابسته هستند، اما تجسم تأثیر تغییر هر عنصر خاص کار ساده ای نیست. شبیه سازی چنین ساختارهای پیچیده ای از لحاظ محاسباتی اغلب پر هزینه بوده و احتمالاً ساعت ها برای اجرای آن طول می کشد. روش Nelder - Mead، در نوع اصلی نیاز به بیش از دو ارزیابی در هر تکرار ندارد، به جز عملیات منقبض شدن که در ادامه شرح داده شده است، که در مقایسه با برخی دیگر از روش های بهینه سازی جستجوی مستقیم، مورد توجه است. با این حال، مجموع تعداد تکرارها، ممکن است از حد مطلوب پیشنهادی بیشتر باشد.
روش نلدر – مید در یک مسئله n بعدی، مجموعه از n+1 نقطه آزمایشی که به صورت سیمپلکس است را در نظر می گیرد. سپس به منظور پیدا کردن یک نقطه آزمایشی جدید و جایگزینی یکی از نقاط آزمایشی قدیمی با مورد جدید، رفتا تابع مورد نظر در هر نقطه آزمایشی، مورد بررسی قرار می گیرد و سپس این روش ادمه پیدا می کند. ساده ترین رویکرد جایگزینی بدترین نقطه، از لحاظ مقدار، با یک نقطه منعکس شده، از طریق مرکز n نقطه باقی مانده می باشد. اگر این نقطه منعکس شده بهتر از نقطه فعلی باشد، می توانیم کشیدگی را در امتداد این خط امتحان کنیم. از طرفی دیگر، اگر این نکته جدید بهتر از مقدار نقطه قبلی نباشد، در واقع ما در یک دره قدم می گذاریم، بنابراین سیمپلکس را در جهت بدست آوردن یک نقطه بهتر منقبض می کنیم. توضیح شهودی الگوریتم از "دستور العمل های عددی":[ ۵]




wiki: روش نلدر مید
