روش دوبخشی ( به انگلیسی: Bisection method ) یا تصنیف، یکی از روش های مهم مطرح شده در محاسبات عددی برای یافتن ریشه یک تابع پیوسته است که می دانیم در دو نقطه مقدار آن دارای علامت مختلف است. تکرار این روش بر روی تابع هایی با ویژگی ذکر شده در صورتی که در حدود بازه، هم علامت نباشند ما را به ریشه می رساند. [ ۱]
به طور دقیقتر ابتدا مقدار تابع در میانه بازه داده شده محاسبه می شود، سپس از بین دو بازه ایجاد شده، بازه ای انتخاب می شود که مقدار تابع در ابتدا و انتهای بازهٔ جدید هم علامت نباشند.
در این صورت به علت پیوستگی تابع اطمینان داریم ریشه در این بازه خواهد بود. حال برای این بازهٔ منتخب دوباره الگوریتم را تکرار می کنیم و به ریشه نزدیکتر می شویم.
این روش در محاسبات عددی از ساده ترین روش های پیدا کردن ریشه تابع است. محاسبات ساده ای دارد و نیاز به محاسبات دشوار مشتق و انتگرال ندارد. از طرفی در کنار سادگی، این روش کند است و نسبت به بقیه روش های پیشنهادی برای پیدا کردن ریشه یک تابع، دیرتر به جواب می رسد.
روش دوبخشی که بعضاً روش تصنیف نیز خوانده می شود، شباهت هایی به الگوریتم جستجوی دودویی در علوم کامپیوتر دارد.
داده های مسئله عبارتند از ( f ( x به عنوان تابع ورودی و بازه که در آن به دنبال ریشه تابع هستیم.
دو محدودیت اصلی برای به کارگیری از این روش وجود دارد:
• در بازه داده شده، ریشه وجود داشته باشد.
• ریشه ذکر شده در بازه فوق یکتا باشد.
اگر بخواهیم محدودیت های گفته شده را به زبان ریاضی بیان کنیم، اینگونه خواهد بود:
• مقدار تابع در x=a و x=b هم علامت نباشند، به عبارتی f ( a ) . f ( b ) < 0.
• با توجه به قضیه مقدار میانی و شروط ۱ و ۲ حتماً X در بازه وجود دارد که f ( X ) = ۰ باشد.
• در هیچ یک از نقاط بازه مشتق تابع ( f ( x برابر صفر نباشد. [ ۲]
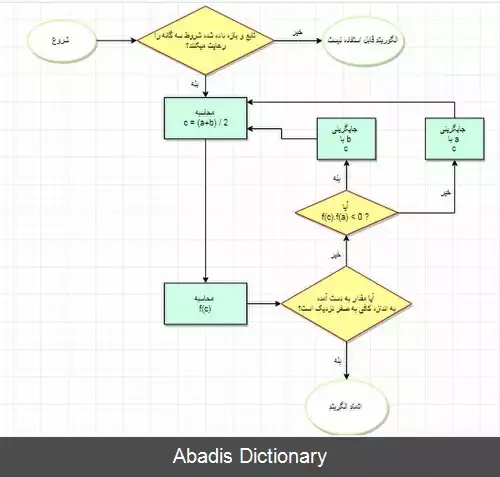
• محاسبه مقدار c - نقطه وسط بازه - یا به عبارتی a+b ) = c ) ½.
• محاسبه مقدار تابع در f ( c ) , c.
• اگر c به قدر کافی به ریشه نزدیک بود ( مقدار | ( f ( c ) | به اندازه کافی به صفر نزدیک بود ) ، محاسبات را متوقف می کنیم.
• در غیر این صورت اگر ( f ( c هم علامت ( f ( a بود c را جایگزین a می کنیم، در غیر این صورت ( یعنی اگر ( f ( c هم علامت ( f ( b بود ) c را جایگزین b می کنیم. در این حالت مطمئنیم ریشه در بازه جدید وجود خواهد داشت و دوباره به مرحله ۱ برمی گردیم.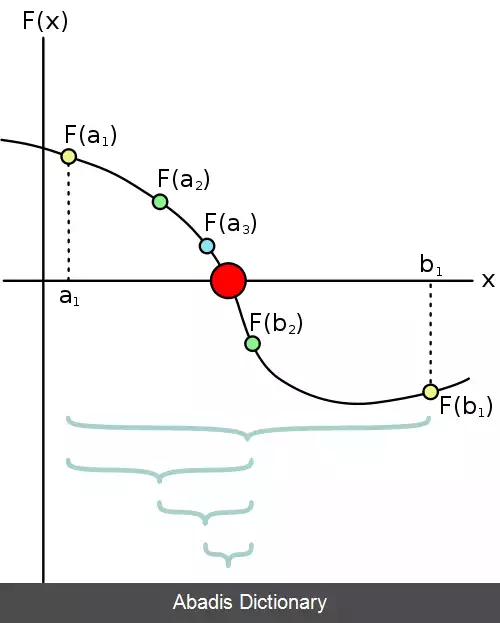
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه طور دقیقتر ابتدا مقدار تابع در میانه بازه داده شده محاسبه می شود، سپس از بین دو بازه ایجاد شده، بازه ای انتخاب می شود که مقدار تابع در ابتدا و انتهای بازهٔ جدید هم علامت نباشند.
در این صورت به علت پیوستگی تابع اطمینان داریم ریشه در این بازه خواهد بود. حال برای این بازهٔ منتخب دوباره الگوریتم را تکرار می کنیم و به ریشه نزدیکتر می شویم.
این روش در محاسبات عددی از ساده ترین روش های پیدا کردن ریشه تابع است. محاسبات ساده ای دارد و نیاز به محاسبات دشوار مشتق و انتگرال ندارد. از طرفی در کنار سادگی، این روش کند است و نسبت به بقیه روش های پیشنهادی برای پیدا کردن ریشه یک تابع، دیرتر به جواب می رسد.
روش دوبخشی که بعضاً روش تصنیف نیز خوانده می شود، شباهت هایی به الگوریتم جستجوی دودویی در علوم کامپیوتر دارد.
داده های مسئله عبارتند از ( f ( x به عنوان تابع ورودی و بازه که در آن به دنبال ریشه تابع هستیم.
دو محدودیت اصلی برای به کارگیری از این روش وجود دارد:
• در بازه داده شده، ریشه وجود داشته باشد.
• ریشه ذکر شده در بازه فوق یکتا باشد.
اگر بخواهیم محدودیت های گفته شده را به زبان ریاضی بیان کنیم، اینگونه خواهد بود:
• مقدار تابع در x=a و x=b هم علامت نباشند، به عبارتی f ( a ) . f ( b ) < 0.
• با توجه به قضیه مقدار میانی و شروط ۱ و ۲ حتماً X در بازه وجود دارد که f ( X ) = ۰ باشد.
• در هیچ یک از نقاط بازه مشتق تابع ( f ( x برابر صفر نباشد. [ ۲]
• محاسبه مقدار c - نقطه وسط بازه - یا به عبارتی a+b ) = c ) ½.
• محاسبه مقدار تابع در f ( c ) , c.
• اگر c به قدر کافی به ریشه نزدیک بود ( مقدار | ( f ( c ) | به اندازه کافی به صفر نزدیک بود ) ، محاسبات را متوقف می کنیم.
• در غیر این صورت اگر ( f ( c هم علامت ( f ( a بود c را جایگزین a می کنیم، در غیر این صورت ( یعنی اگر ( f ( c هم علامت ( f ( b بود ) c را جایگزین b می کنیم. در این حالت مطمئنیم ریشه در بازه جدید وجود خواهد داشت و دوباره به مرحله ۱ برمی گردیم.


wiki: روش دوبخشی
