روش تبدیل معکوس برای شبیه سازی متغیر تصادفی ( نام علمی: Inverse transform sampling یا Inverse transformation method ( همچنین شناخته شده تحت عناوین ( inverse probability integral transform, Smirnov transform, universality of the uniform, یا golden rule[ ۱] ) ) یکی از روش های عمومی برای شبیه سازی متغیرهای تصادفی روش تبدیل معکوس می باشد. گزاره: فرض کنید U یک متغیر تصادفی یکنواخت روی فاصله ( ۱و۰ ) باشد. برای هر تابع توزیع تجمعی پیوسته F اگر متغیر تصادفی Y را به وسیله Y=F^ ( - 1 ) ( U ) تعریف کنیم، آنگاه متغیر تصادفی Y دارای تابع توزیع تجمعی F است. ( F^ ( - 1 ) ( x ) برابر آن مقدار y که F ( y ) =x است تعریف می شود.
F_Y ( a ) =P{Y≤a} =P{F^ ( - 1 ) ( U ) ≤a} حال چون F ( x ) تابعی یکنواست، نتیجه می شود که F^ ( - 1 ) ( U ) ≤a اگر و فقط اگر U≤F ( a ) . بدین ترتیب داریم: F_Y ( a ) =P{U≤F ( a ) } F ( a ) نتیجه می شود که می توان متغیر تصادفی X را دارای تابع توزیع تجمعی پیوسته F است به وسیله تولید یک عدد تصادفی U و اختیار 〖X=F〗^ ( - 1 ) ( U ) شبیه سازی کرد.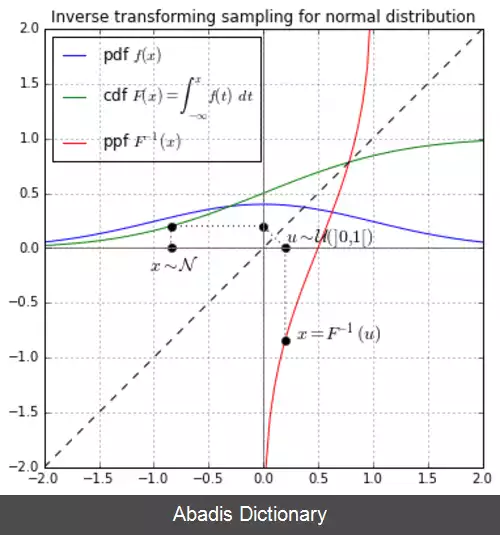
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفF_Y ( a ) =P{Y≤a} =P{F^ ( - 1 ) ( U ) ≤a} حال چون F ( x ) تابعی یکنواست، نتیجه می شود که F^ ( - 1 ) ( U ) ≤a اگر و فقط اگر U≤F ( a ) . بدین ترتیب داریم: F_Y ( a ) =P{U≤F ( a ) } F ( a ) نتیجه می شود که می توان متغیر تصادفی X را دارای تابع توزیع تجمعی پیوسته F است به وسیله تولید یک عدد تصادفی U و اختیار 〖X=F〗^ ( - 1 ) ( U ) شبیه سازی کرد.

wiki: روش تبدیل معکوس
