روش اِفْنا ( مأخوذ از واژه عربی إِفْناء ) ( به انگلیسی: method of exhaustion ) روشی برای یافتن مساحت یک شکل با محاط کردن دنباله ای از چندضلعی ها در آن است به گونه ای که مساحت آن چندضلعی ها به سمت مساحت شکل مورد نظر همگرا شود. اگر دنباله به درستی ساخته شده باشد، با افزایش n، تفاضل مساحت چندضلعی nام و شکل مورد نظر به اندازهٔ دلخواه کوچک خواهد شد. همان طور که این تفاضل به اندازهٔ دلخواه کوچک می شود، مقادیر احتمالی برای مساحت شکل مورد نظر توسط کران پایین دنبالهٔ مساحت ها به نحوی سازمان یافته «اِفنا می شوند». [ ۱] این ایده از آنتیفون در قرن پنجم پیش از میلاد نشئت می گیرد اما کاملاً مشخص نیست که او به چه میزان درک درستی از این روش داشته است. چند قرن بعد، اودوکسوس کنیدوسی تئوری این ایده را به طرزی دقیق بیان کرد. گریگوری د سینت - وینسنت در سال ۱۶۴۷ برای اولین بار در کتاب Opus geometricum quadraturae circuli et sectionum از اصطلاح «اِفنا» استفاده کرد.
مساحت دایره بر اساس محیط و شعاع آن تعیین می شود. اگر یک دایرهٔ مفروض به چهار قطاع مساوی تقسیم شود:
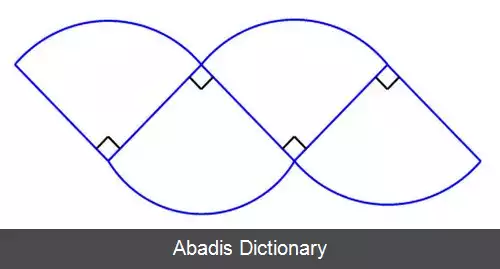
و به صورت زیر کنار هم چیده شود:
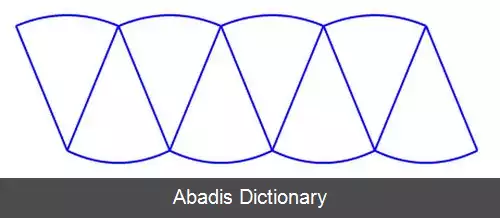
مشاهده می شود که شکل حاصل نامتعارف است. اما اگر دایرهٔ مفروض به قطاع های بیشتری تقسیم شود و همین روند ادامه یابد، مشاهده می شود که شکل به دست آمده به متوازی الاضلاع نزدیک می شود. به عنوان نمونه در مرحله ای که دایره مفروض به هشت قطاع مساوی تقسیم می شود، حاصل شکل زیر خواهد بود ( که به متوازی الاضلاع نزدیک تر است ) :
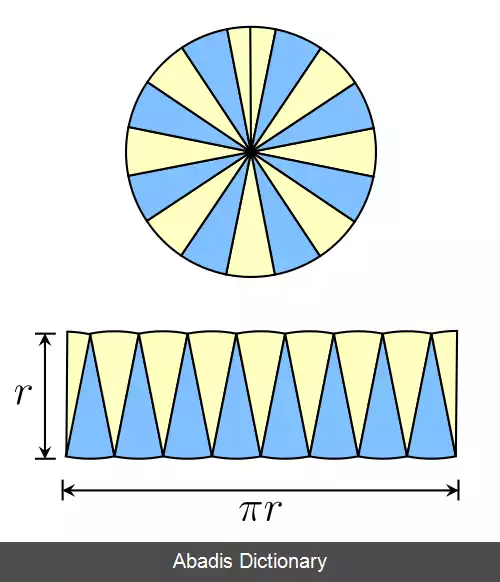
اگر فرض را بر این باشد که دایره به تعداد بی شمار قطاع مساوی مساوی تقسیم شده است، آن گاه شکل حاصل متوازی الاضلاعی خواهد بود که به مستطیل خیلی نزدیک است. [ ۲] با دانستن اینکه مساحت این متوازی الاضلاع با دایرهٔ مفروض برابر است، با ضرب کردن ارتفاع متوازی الاضلاع ( که همان شعاع دایره است ) در ضلع بزرگ متوازی الاضلاع مساحت دایره به دست می آید. قابل توجه است که اضلاع بزرگ متوازی الاضلاع همان کمان های نظیر قطاع ها را تشکیل می دهند؛ پس می شود گفت که هر ضلع بزرگ متوازی الاضلاع برابر با نصف محیط دایرهٔ مفروض خواهد بود؛ یعنی اندازهٔ آن C 2 = 2 π r 2 = π r خواهد بود. اندازهٔ ضلع کوچک متوازی الاضلاع هم که r ( شعاع دایره ) است، پس مساحت دایره A = r × π r = π r 2 خواهد بود. [ ۳] وی روش افنا را تا 96 ضلعی انجام داد.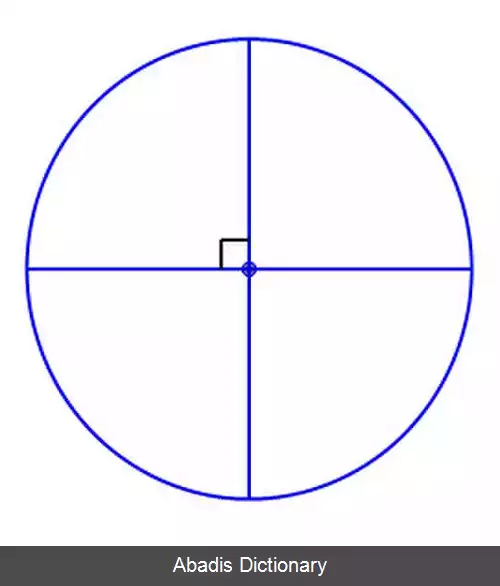
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمساحت دایره بر اساس محیط و شعاع آن تعیین می شود. اگر یک دایرهٔ مفروض به چهار قطاع مساوی تقسیم شود:
و به صورت زیر کنار هم چیده شود:
مشاهده می شود که شکل حاصل نامتعارف است. اما اگر دایرهٔ مفروض به قطاع های بیشتری تقسیم شود و همین روند ادامه یابد، مشاهده می شود که شکل به دست آمده به متوازی الاضلاع نزدیک می شود. به عنوان نمونه در مرحله ای که دایره مفروض به هشت قطاع مساوی تقسیم می شود، حاصل شکل زیر خواهد بود ( که به متوازی الاضلاع نزدیک تر است ) :
اگر فرض را بر این باشد که دایره به تعداد بی شمار قطاع مساوی مساوی تقسیم شده است، آن گاه شکل حاصل متوازی الاضلاعی خواهد بود که به مستطیل خیلی نزدیک است. [ ۲] با دانستن اینکه مساحت این متوازی الاضلاع با دایرهٔ مفروض برابر است، با ضرب کردن ارتفاع متوازی الاضلاع ( که همان شعاع دایره است ) در ضلع بزرگ متوازی الاضلاع مساحت دایره به دست می آید. قابل توجه است که اضلاع بزرگ متوازی الاضلاع همان کمان های نظیر قطاع ها را تشکیل می دهند؛ پس می شود گفت که هر ضلع بزرگ متوازی الاضلاع برابر با نصف محیط دایرهٔ مفروض خواهد بود؛ یعنی اندازهٔ آن C 2 = 2 π r 2 = π r خواهد بود. اندازهٔ ضلع کوچک متوازی الاضلاع هم که r ( شعاع دایره ) است، پس مساحت دایره A = r × π r = π r 2 خواهد بود. [ ۳] وی روش افنا را تا 96 ضلعی انجام داد.




wiki: روش افنا
