اعتبارسنجی متقابل، [ ۱] یک روش ارزیابی مدل است که تعیین می نماید نتایج یک تحلیل آماری بر روی یک مجموعه داده تا چه اندازه قابل تعمیم و مستقل از داده های آموزشی است. این روش به طور ویژه در کاربردهای پیش بینی مورد استفاده قرار می گیرد تا مشخص شود مدل موردنظر تا چه اندازه در عمل مفید خواهد بود. به طور کلی یک دور از اعتبارسنجی ضربدری شامل افراز داده ها به دو زیرمجموعه مکمل، انجام تحلیل بر روی یکی از آن زیرمجموعه ها ( داده های آموزشی ) و اعتبارسنجی تحلیل با استفاده از داده های مجموعه دیگر است ( داده های اعتبارسنجی یا آزمایش ) . برای کاهش پراکندگی، عمل اعتبارسنجی چندین بار با افرازهای مختلف انجام و از نتایج اعتبارسنجی ها میانگین گرفته می شود. در اعتبارسنجی متقابل K لایه، داده ها به K زیرمجموعه افراز می شوند. از این K زیرمجموعه، هر بار یکی برای اعتبارسنجی و K - 1 تای دیگر برای آموزش بکار می روند. این روال K بار تکرار می شود و همه داده ها دقیقاً یک بار برای آموزش و یک بار برای اعتبارسنجی بکار می روند. در نهایت میانگین نتیجه این K بار اعتبارسنجی به عنوان یک تخمین نهایی برگزیده می شود. به طور معمول از روش اعتبارسنجی پنج لایه یا ده لایه در پژوهش های مدل سازی و پیش بینی استفاده می شود.
فرض کنید ما یک مدل با یک یا چند پارامتر ناشناخته داریم و یک مجموعه داده که مدل مناسب است ( مدل آموزشی ) . اگر ما یک نمونه مستقل از داده های اعتبارسنجی از همان جمعیت را به عنوان داده های آموزش در نظر بگیریم، به طور کلی معلوم می شود که این مدل داده های اعتبارسنجی متناسب با داده های آموزش نیست. اندازه این تفاوت احتمالاً بزرگ است، به خصوص اگر اندازه مجموعه داده های آموزشی کوچک باشد یا زمانی که تعداد پارامترهای موجود در مدل بزرگ باشد. اعتبارسنجی متقابل یک راه برای برآورد اندازه این اثر است. در رگرسیون خطی، مقادیر پاسخ واقعی y 1 . . . y n و n تا بردار p بعدی واریانس x 1 . . . x n را داریم. اجزای هر بردار x i به صورت x i 1 . . . x i p است. اگر ما از کمترین مربعات برای متناسب سازی یک تابع به صورت ابرصفحهٔ y = α + β T x به داده های ( x i , y i ) 1 ≤ i ≤ n استفاده کنیم، در واقع از خطای میانگین مربعات استفاده کرده ایم. این خطا برای پارامتر تخمین زده شده a به صورت زیر است:
1 n ∑ i = 1 n ( y i − a − β T x i ) 2 = 1 n ∑ i = 1 n ( y i − a − β 1 x i 1 − ⋯ − β p x i p ) 2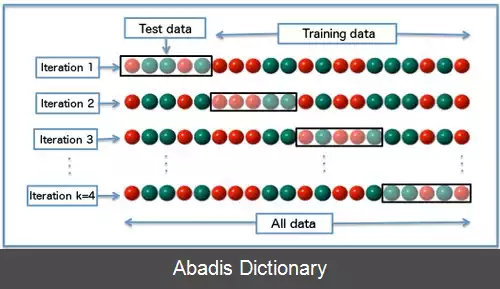
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنید ما یک مدل با یک یا چند پارامتر ناشناخته داریم و یک مجموعه داده که مدل مناسب است ( مدل آموزشی ) . اگر ما یک نمونه مستقل از داده های اعتبارسنجی از همان جمعیت را به عنوان داده های آموزش در نظر بگیریم، به طور کلی معلوم می شود که این مدل داده های اعتبارسنجی متناسب با داده های آموزش نیست. اندازه این تفاوت احتمالاً بزرگ است، به خصوص اگر اندازه مجموعه داده های آموزشی کوچک باشد یا زمانی که تعداد پارامترهای موجود در مدل بزرگ باشد. اعتبارسنجی متقابل یک راه برای برآورد اندازه این اثر است. در رگرسیون خطی، مقادیر پاسخ واقعی y 1 . . . y n و n تا بردار p بعدی واریانس x 1 . . . x n را داریم. اجزای هر بردار x i به صورت x i 1 . . . x i p است. اگر ما از کمترین مربعات برای متناسب سازی یک تابع به صورت ابرصفحهٔ y = α + β T x به داده های ( x i , y i ) 1 ≤ i ≤ n استفاده کنیم، در واقع از خطای میانگین مربعات استفاده کرده ایم. این خطا برای پارامتر تخمین زده شده a به صورت زیر است:
1 n ∑ i = 1 n ( y i − a − β T x i ) 2 = 1 n ∑ i = 1 n ( y i − a − β 1 x i 1 − ⋯ − β p x i p ) 2

wiki: روش اعتبارسنجی متقابل
