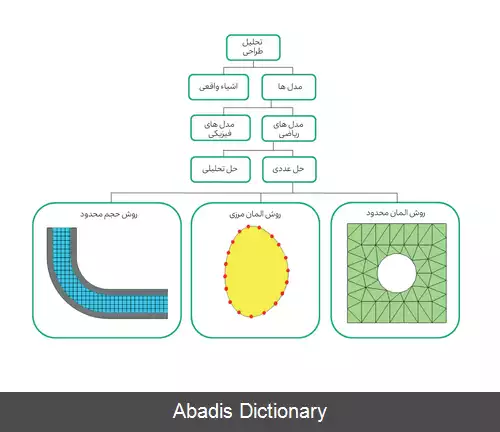
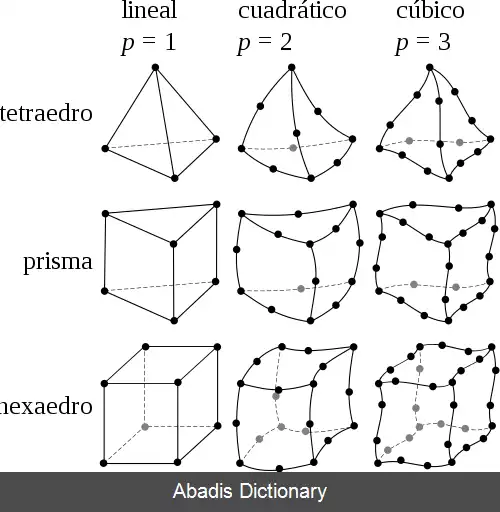
روش اجزاء محدود یا روش المان محدود ( به انگلیسی: Finite Element Method ) که به اختصار FEM نامیده می شود، رایج ترین روش عددی برای حل مسائل مهندسی و مدل های ریاضیاتی است. رایج ترین این مسائل شامل تحلیل سازه ها، انتقال گرما، دینامیک شاره ها، انتقال جرم و پتانسیل الکترومغناطیسی می شود. روش المان محدود، روشی عددی برای حل معادلات دیفرانسیلی جزئی یا PDE تعریف شده بر اساس یک یا دو متغیر مکانی است. در این روش، برای حل مسئله یک سیستم بزرگ به قسمت های کوچک تر و ساده تر به نام المان های محدود تقسیم می شود. این گسسته سازی مکانی مستلزم تعریف جسم یا محیط مسئله بصورت یک شبکه یا در اصطلاح مش است. در واقع شبکه از مجموعه ای از نقاط گسسته برای تبدیل جسم یا محیط مسئله به محدودهٔ عددی برای حل مسئله است. فرمول بندی روش المان محدود در ادامه به سیستمی از معادلات جبری تبدیل می شود که بیانگر تقریبی از یک تابع مجهول بر روی هر المان است. [ ۱] سپس معادلات ساده ای که هر یک از این المان ها را مدلسازی می کنند، در قالب یک سیستم بزرگتر از معادلات که کل محدودهٔ مسئله را در بر می گیرد، سرهم بندی می شوند. در نهایت با استفاده از حساب تغییرات جوابی برای مسئله با به حداقل رساندن یک تابع خطا یافته می شود. کاربرد عملی اجزای محدود معمولاً با نام تحلیل اجزا محدود ( به انگلیسی: Finite Element Analysis ) یا به اختصار FEA خوانده می شود.
نرم افزارهای تحلیل المان محدود ( FEA ) طراحان و مهندسان را قادر می سازد تا به صورت دیجیتالی رفتار سازه ها و اجزای مکانیکی را آزمایش و پیش بینی کنند و مسائل پیچیده مهندسی تحت شرایط بارگذاری استاتیکی و دینامیکی را حل کنند. FEM به عنوان پایه نرم افزارهای شبیه سازی مدرن استفاده می شود و به مهندسان کمک می کند تا مناطق تنش، نقاط ضعف و غیره را در طراحی های خود پیدا کنند. نتایج یک شبیه سازی مبتنی بر نرم افزار FEA معمولاً از طریق یک مقیاس رنگی نشان داده می شود که به عنوان مثال، توزیع فشار روی جسم را نشان می دهد. [ ۲]
در دهه ۱۹۶۰ که آنالیزهای عددی برای اولین بار در کاربردهای مهندسی معرفی شدند، از روش های تحلیل بسیاری استفاده شد، اما با گذشت زمان، روش المان محدود یا FEM به دلیل عمومیت و کارایی عددی آن به روش عددی غالب تبدیل شد. با اینکه روش های دیگر مزیت هایی را در کاربردهای خاص دارند، اما اِعمال آنها برای انواع دیگر تحلیل ها دشوار یا غیرممکن است. در عین حال، FEM را می توان تقریباً برای هر نوع تحلیلی اعمال کرد. این کلیت و کارایی عددی برای برنامه نویسانی که می خواهند تصمیم بگیرند از کدام روش در برنامه تحلیل تجاری خود استفاده کنند، مورد توجه قرار می گیرد. توسعه یک نرم افزار تحلیل مدرن متشکل از چندین میلیون خط کد، سرمایه گذاری عظیمی است که تنها با ایجاد یک محصول همه کاره و کارآمد قابل جبران است. FEM این تطبیق پذیری و کارایی را ارائه می دهد و به همین دلیل بر بازار نرم افزارهای تحلیل تجاری تسلط پیدا کرده است. [ ۳]
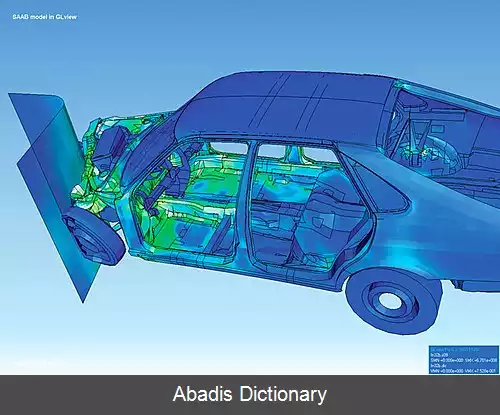


این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنرم افزارهای تحلیل المان محدود ( FEA ) طراحان و مهندسان را قادر می سازد تا به صورت دیجیتالی رفتار سازه ها و اجزای مکانیکی را آزمایش و پیش بینی کنند و مسائل پیچیده مهندسی تحت شرایط بارگذاری استاتیکی و دینامیکی را حل کنند. FEM به عنوان پایه نرم افزارهای شبیه سازی مدرن استفاده می شود و به مهندسان کمک می کند تا مناطق تنش، نقاط ضعف و غیره را در طراحی های خود پیدا کنند. نتایج یک شبیه سازی مبتنی بر نرم افزار FEA معمولاً از طریق یک مقیاس رنگی نشان داده می شود که به عنوان مثال، توزیع فشار روی جسم را نشان می دهد. [ ۲]
در دهه ۱۹۶۰ که آنالیزهای عددی برای اولین بار در کاربردهای مهندسی معرفی شدند، از روش های تحلیل بسیاری استفاده شد، اما با گذشت زمان، روش المان محدود یا FEM به دلیل عمومیت و کارایی عددی آن به روش عددی غالب تبدیل شد. با اینکه روش های دیگر مزیت هایی را در کاربردهای خاص دارند، اما اِعمال آنها برای انواع دیگر تحلیل ها دشوار یا غیرممکن است. در عین حال، FEM را می توان تقریباً برای هر نوع تحلیلی اعمال کرد. این کلیت و کارایی عددی برای برنامه نویسانی که می خواهند تصمیم بگیرند از کدام روش در برنامه تحلیل تجاری خود استفاده کنند، مورد توجه قرار می گیرد. توسعه یک نرم افزار تحلیل مدرن متشکل از چندین میلیون خط کد، سرمایه گذاری عظیمی است که تنها با ایجاد یک محصول همه کاره و کارآمد قابل جبران است. FEM این تطبیق پذیری و کارایی را ارائه می دهد و به همین دلیل بر بازار نرم افزارهای تحلیل تجاری تسلط پیدا کرده است. [ ۳]






wiki: روش اجزاء محدود
