رنگ آمیزی آزمند. الگوریتم رنگ آمیزی آزمند ( حریصانه ) ( به انگلیسی: Greedy coloring ) در میان مسائل گوناگون رنگ آمیزی گراف، یک الگوریتم آزمند برای رنگ آمیزی رئوس یک گراف می باشد. این روش رئوس گراف را بر اساس ترتیب مشخصی انتخاب کرده و تلاش می کند با رنگ هایی که در رنگ آمیزی رئوس قبلی به کار رفته آن را به گونه ای رنگ کند که هیچ دو راس مجاوری دارای رنگ یکسان نباشند. در صورتی که امکان استفاده از رنگ های پیشین نباشد یک رنگ جدید به مجموعه رنگ ها اضافه می شود. اگرچه با استفاده از این الگوریتم در همه حالات جواب بهینه برای مسائل رنگ آمیزی بدست نخواهد آمد اما به طور کلی از آن برای کمینه کردن تعداد رنگ های لازم برای رنگ آمیزی گراف استفاده می شود. این الگوریتم از دو قسمت اصلی تشکیل شده است: مرتب سازی رئوس و مرتب سازی رنگ ها
معمولاً الگوریتم رنگ آمیزی آزمند، بدترین عملکرد خود را بر روی گراف های کامل دوبخشی k n, n دارد که یال نظیر رئوس xi و xj که i=j حذف شده اند.
در صورتی که پس از شماره گذاری رئوس، دو راسی که در یک یال حذف شده قرار دارند به صورت متوالی شماره گذاری شوند، چنین گرافی با n رنگ، رنگ آمیزی می شود درحالیکه یک گراف ۲ - رنگ پذیر است؛ بنابراین ترتیب رئوس در الگوریتم آزمند اهمیت فراوانی دارد.
یکی از روش های معمول شماره گذاری رئوس، انتساب کمترین اولویت به راس با کمترین درجه و مرتب سازی بقیه رئوس به همین شکل است. اگر هر زیرگراف یک گراف دارای بیشینه درجه d باشد الگوریتم حریصانه حداکثر از d+۱ رنگ استفاده می کند.
برای گرافی با بیشینه درجه D الگوریتم حریصانه از حداکثر D+۱ رنگ استفاده می کند. قضیه بروک[ ۱] نشان می دهد این تعداد با دو استثنا ( گراف های cliques, odd cycle ) حداکثر برابر D است. یکی از روش های اثبات این نظریه، شماره گذاری رئوس به صورتیست که دو راس اول، مجاور راس نهایی بوده ولی با یکدیگر مجاور نباشند بنابراین تعداد رنگ های استفاده شده الگوریتم آزمند برابر D خواهد بود. پاسخ به این سؤال که آیا برای گراف مفروض G وعدد مفروض K یک الگوریتم آزمند وجود دارد که گراف را با کمتر از K رنگ، رنگ آمیزی کند یا خیر یک مسئله NP - Complete است.
تعدادی از معروف ترین الگوریتم های شماره گذاری رئوس عبارتند از:
ترتیب خاص از پیش تعیین شده ( SPECIFIC - PREDEFINED - ORDERING:SP )
ترتیب کاهش درجه نودها ( DECREASING DEGREE ORDERING: DD ) به عبارت دیگر هر بار راس رنگ نشده با بزرگترین درجه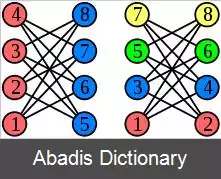

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمعمولاً الگوریتم رنگ آمیزی آزمند، بدترین عملکرد خود را بر روی گراف های کامل دوبخشی k n, n دارد که یال نظیر رئوس xi و xj که i=j حذف شده اند.
در صورتی که پس از شماره گذاری رئوس، دو راسی که در یک یال حذف شده قرار دارند به صورت متوالی شماره گذاری شوند، چنین گرافی با n رنگ، رنگ آمیزی می شود درحالیکه یک گراف ۲ - رنگ پذیر است؛ بنابراین ترتیب رئوس در الگوریتم آزمند اهمیت فراوانی دارد.
یکی از روش های معمول شماره گذاری رئوس، انتساب کمترین اولویت به راس با کمترین درجه و مرتب سازی بقیه رئوس به همین شکل است. اگر هر زیرگراف یک گراف دارای بیشینه درجه d باشد الگوریتم حریصانه حداکثر از d+۱ رنگ استفاده می کند.
برای گرافی با بیشینه درجه D الگوریتم حریصانه از حداکثر D+۱ رنگ استفاده می کند. قضیه بروک[ ۱] نشان می دهد این تعداد با دو استثنا ( گراف های cliques, odd cycle ) حداکثر برابر D است. یکی از روش های اثبات این نظریه، شماره گذاری رئوس به صورتیست که دو راس اول، مجاور راس نهایی بوده ولی با یکدیگر مجاور نباشند بنابراین تعداد رنگ های استفاده شده الگوریتم آزمند برابر D خواهد بود. پاسخ به این سؤال که آیا برای گراف مفروض G وعدد مفروض K یک الگوریتم آزمند وجود دارد که گراف را با کمتر از K رنگ، رنگ آمیزی کند یا خیر یک مسئله NP - Complete است.
تعدادی از معروف ترین الگوریتم های شماره گذاری رئوس عبارتند از:
ترتیب خاص از پیش تعیین شده ( SPECIFIC - PREDEFINED - ORDERING:SP )
ترتیب کاهش درجه نودها ( DECREASING DEGREE ORDERING: DD ) به عبارت دیگر هر بار راس رنگ نشده با بزرگترین درجه


wiki: رنگ آمیزی آزمند
