در حوزهٔ فشرده سازی داده ها، کدینگ یا کدگذاری شانون - فانو، که به افتخار کلود شانون و رابرت فانو این چنین نامیده شده، تکنیکی است، برای ایجاد یک کد پیشوندی ( Prefix Code ) ، بر مبنای مجموعه ای از نمادها و احتمالات ( تخمین زده شده یا اندازه گیری شده ) . این تکنیک نیمه بهینه است؛ چرا که مانند کدگذاری هافمن ، به کمترین طول قابل انتظار کلمات کد ( Codewords ) نمی رسد؛ با این حال بر خلاف کدگذاری هافمن، تضمین می کند که تمام طول های کلمات کد در یک بیت از مقدار تئوری ایده آل –logP ( x ) جای می گیرد. این روش در «نظریهٔ ریاضیِ ارتباطات»، مقاله شانون در سال ۱۹۴۸ در معرفی حوزهٔ نظریه اطلاعات مطرح شده است. این روش بعدها به فانو نسبت داده شد. کدگذاری شانون - فانو نباید با کدگذاری شانون اشتباه شود که روشی است برای اثبات نظریه کدگذاری بدون اختلال شانون و همچنین نباید آن را با کدگذاری شانون - فانو - الیاس ( که به کدگذاری الیاس معروف است ) اشتباه گرفت که پیش ساز کدگذاری محاسباتی است.
در کدگذاری شانون - فانو، نمادها به ترتیب احتمال از زیاد به کم مرتب شده اند؛ و پس از آن به دو مجموعه که احتمال کل شان تا حد ممکن به هم نزدیک است تقسیم می شوند. سپس اولین رقم کد همهٔ نمادها به آن ها اختصاص داده می شود؛ نمادها در مجموعهٔ اول "۰" و در مجموعهٔ دوم "۱" می گیرند. تا زمانی که مجموعه ای با بیش از یک عضو باقی بماند، همین فرایند برای تعیین ارقام متوالی کدهایشان، روی آن ها تکرار می شود. وقتی یک مجموعه به یک نماد کاهش پیدا کند بدان معناست که کد آن نماد کامل است و پیشوند هیچ کدِ نماد دیگری را تشکیل نمی دهد. این الگوریتم کدگذاری های با طول متغیر نسبتاً کارامدی تولید می کند. وقتی دو مجموعهٔ کوچک تر که با یک تقسیم بندی ایجاد شده اند در واقع دارای احتمال برابری هستند، یک بیت اطلاعاتی که برای تمایز آن ها استفاده می شود، به بهینه ترین نحو به کار گرفته می شود. متأسفانه شانون - فانو همیشه پیشوند کدهای بهینه تولید نمی کند؛ مجموعهٔ احتمالات {۰٫۳۵٬۰٫۱۷٬۰٫۱۷٬۰٫۱۶٬۰٫۱۵} مثالی است که به آن کدهای نابهینه ای توسط کدگذاری شانون - فانو اخصاص داده می شود.
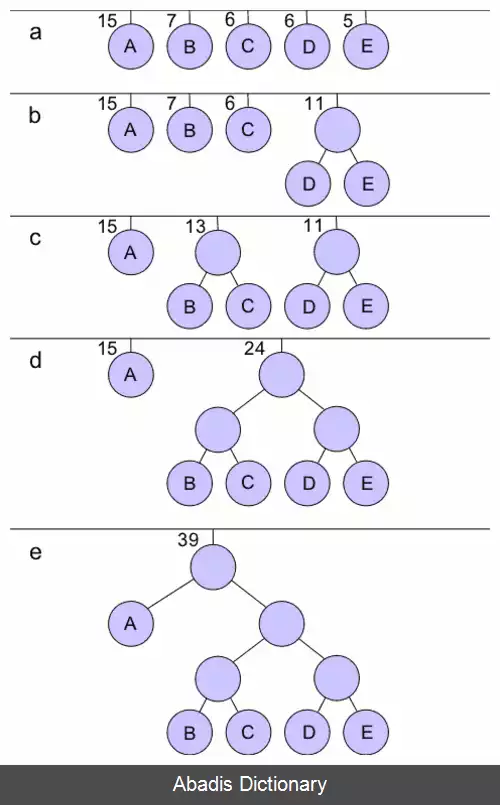
به همین دلیل، شانون - فانو تقریباً هیچ وقت استفاده نمی شود. کدگذاری هافمن تقریباً از نظر محاسباتی ساده است و تحت محدودیت هایی که هر نماد با یک کد متشکل از تعداد درست و جدایی ناپذیری از بیت ها نمایش داده می شود، کدهایی پیشوندی تولید می کند که همیشه به کمترین طول قابل انتظار کلمات کد می رسند. از آن جایی که کدها انتها به انتها در توالی های بلند دسته می شوند این محدودیتی است که اغلب غیرضروری است. اگر گروه های کدها را یک جا در نظر بگیریم، کدگذاری نماد به نماد هافمن فقط وقتی بهینه است که احتمالات نمادها مستقل بوده و توانی از یک دوم باشند، مثلاً n ( 2/1 ) . در اکثر شرایط، کدگذاری محاسباتی می تواند در مجموع فشرده سازی بیشتری نسبت به هافمن یا شانون - فانو تولید کند چرا که می تواند در تعداد کوچکی از بیت ها کدگذاری کند که به طور دقیق تری محتوای اطلاعاتی واقعی نماد را تقریب بزند. با این حال آن میزان که هافمن جایگزین شانون - فانو شده است کدگذاری محاسباتی جای هافمن را نگرفته است چرا که هم کدگذاری محاسباتی از لحاظ محاسبات سنگین تر است و هم توسط چند حق امتیاز انحصاری پوشش داده می شود.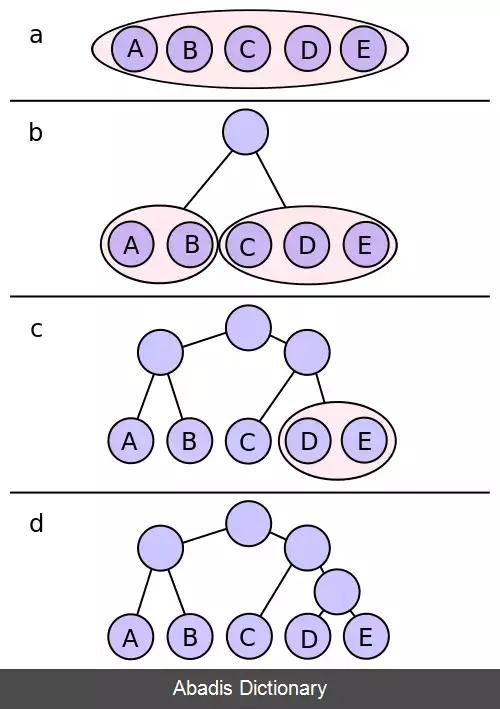
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر کدگذاری شانون - فانو، نمادها به ترتیب احتمال از زیاد به کم مرتب شده اند؛ و پس از آن به دو مجموعه که احتمال کل شان تا حد ممکن به هم نزدیک است تقسیم می شوند. سپس اولین رقم کد همهٔ نمادها به آن ها اختصاص داده می شود؛ نمادها در مجموعهٔ اول "۰" و در مجموعهٔ دوم "۱" می گیرند. تا زمانی که مجموعه ای با بیش از یک عضو باقی بماند، همین فرایند برای تعیین ارقام متوالی کدهایشان، روی آن ها تکرار می شود. وقتی یک مجموعه به یک نماد کاهش پیدا کند بدان معناست که کد آن نماد کامل است و پیشوند هیچ کدِ نماد دیگری را تشکیل نمی دهد. این الگوریتم کدگذاری های با طول متغیر نسبتاً کارامدی تولید می کند. وقتی دو مجموعهٔ کوچک تر که با یک تقسیم بندی ایجاد شده اند در واقع دارای احتمال برابری هستند، یک بیت اطلاعاتی که برای تمایز آن ها استفاده می شود، به بهینه ترین نحو به کار گرفته می شود. متأسفانه شانون - فانو همیشه پیشوند کدهای بهینه تولید نمی کند؛ مجموعهٔ احتمالات {۰٫۳۵٬۰٫۱۷٬۰٫۱۷٬۰٫۱۶٬۰٫۱۵} مثالی است که به آن کدهای نابهینه ای توسط کدگذاری شانون - فانو اخصاص داده می شود.
به همین دلیل، شانون - فانو تقریباً هیچ وقت استفاده نمی شود. کدگذاری هافمن تقریباً از نظر محاسباتی ساده است و تحت محدودیت هایی که هر نماد با یک کد متشکل از تعداد درست و جدایی ناپذیری از بیت ها نمایش داده می شود، کدهایی پیشوندی تولید می کند که همیشه به کمترین طول قابل انتظار کلمات کد می رسند. از آن جایی که کدها انتها به انتها در توالی های بلند دسته می شوند این محدودیتی است که اغلب غیرضروری است. اگر گروه های کدها را یک جا در نظر بگیریم، کدگذاری نماد به نماد هافمن فقط وقتی بهینه است که احتمالات نمادها مستقل بوده و توانی از یک دوم باشند، مثلاً n ( 2/1 ) . در اکثر شرایط، کدگذاری محاسباتی می تواند در مجموع فشرده سازی بیشتری نسبت به هافمن یا شانون - فانو تولید کند چرا که می تواند در تعداد کوچکی از بیت ها کدگذاری کند که به طور دقیق تری محتوای اطلاعاتی واقعی نماد را تقریب بزند. با این حال آن میزان که هافمن جایگزین شانون - فانو شده است کدگذاری محاسباتی جای هافمن را نگرفته است چرا که هم کدگذاری محاسباتی از لحاظ محاسبات سنگین تر است و هم توسط چند حق امتیاز انحصاری پوشش داده می شود.


wiki: رمزگذاری شانون فانو
