رابطه هم ارزی[ ۱] ( به انگلیسی: Equivalence relation ) در ریاضیات یک رابطه دوتایی است که بازتابی، متقارن، و ترایا است.
رابطه ها در ریاضیات به صورت زیرمجموعه هایی از ضرب دکارتی[ ۲] دو یا چند مجموعهٔ مشابه یا متمایز تعریف می شوند. این رابطه ها می توانند خواص و ویژگی های گوناگونی داشته باشند؛ اما ۴ ویژگی از سایر ویژگی ها مهم تر است. رابطه هایی که این خواص را دارند، به این شکل نامیده می شوند:
• بازتابی[ ۳]
• تقارنی[ ۴]
• پادتقارنی
• ترایایی
رابطه ای که بازتابی، تقارنی و ترایایی باشد، رابطهٔ هم ارزی[ ۵] و رابطه ای که بازتابی، پادتقارنی و ترایایی باشد، رابطهٔ ترتیب[ ۶] خوانده می شود.
• رابطهٔ توازی خطوط در صفحه ( || ) : مثالی از رابطهٔ هم ارزی
نشان می دهیم که رابطهٔ توازی خطوط در صفحه، یک رابطهٔ هم ارزی است:
نخست - هر خط با خودش موازی است؛ پس این رابطه بازتابی است.
دوم - اگر خطی با خط دیگری موازی باشد، آن خط نیز با این خط موازی است؛ پس این رابطه تقارنی است.
سوم - اگر خط d با خط 'd، و خط 'd با خط «d موازی باشند، آن گاه بنابر قضایای هندسهٔ اقلیدسی، خط d با خط»d موازی خواهد بود؛ پس این رابطه ترایایی نیز هست.
به این ترتیب مشخص شد که رابطهٔ توازی، یک رابطهٔ هم ارزی است.
• رابطهٔ بزرگ تر مساوی بودن ( ≥ {\displaystyle \geq } ) : مثالی از رابطهٔ ترتیب
نشان می دهیم که رابطهٔ ≥ یک رابطهٔ ترتیب است:
نخست - هر عدد از خودش بزرگ تر یا با خودش مساوی است؛ پس این رابطه بازتابی است.
دوم - اگر a ≥ b و b ≥ a آن گاه نتیجه می شود که a = b ؛ پس این رابطه پادتقارنی است.
سوم - اگر a ≥ b و b ≥ c آن گاه نتیجه می شود که a ≥ c ؛ پس این رابطه ترایایی است.
به این ترتیب مشخص شد که رابطهٔ ≥ یک رابطهٔ ترتیب است.
وقتی یک رابطهٔ هم ارزی را روی مجموعه ای تعریف می کنیم، این رابطه مجموعه را به دسته ( کلاس ) های هم ارزی[ ۷] افراز می کند. به عنوان نمونه، همان مثال توازی خطوط را در نظر بگیرید. این رابطه، رابطه ای هم ارزی است و خطوط موجود در صفحه را به دسته های هم ارزی افراز می کند؛ به طوری که همهٔ خطوط موجود در هر دسته، با هم موازی اند.
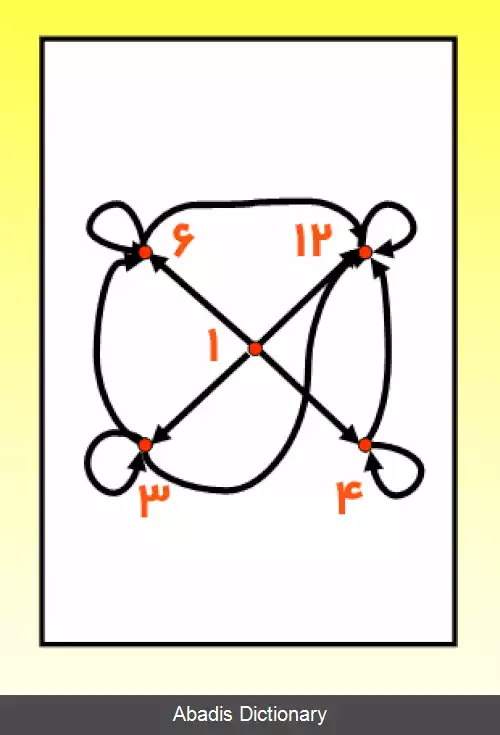
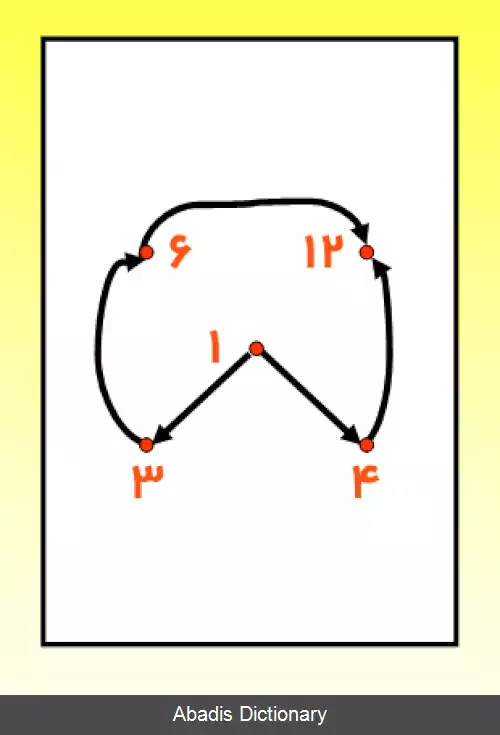
یک مثال مفید دیگر برای درک بهتر دسته های هم ارزی، رابطهٔ هم باقی ماندگی اعداد طبیعی به پیمانه ای مشخص[ ۸] است. نشان دادن این که این رابطه هم ارزی ست، بسیار ساده است و لذا از اثبات آن می گذریم. به این ترتیب همان طور که گفته شد، این رابطه مجموعهٔ اعداد طبیعی را به دسته های هم ارزی افراز خواهد کرد. اعداد موجود در هریک از این دسته ها، به پیمانهٔ m باقی ماندهٔ یکسانی خواهند داشت.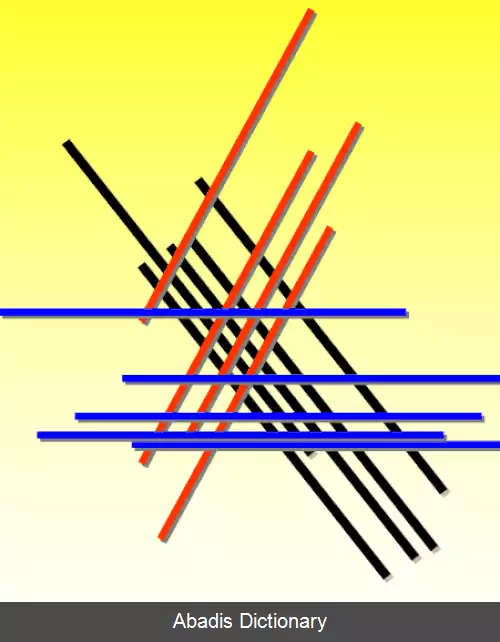

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفرابطه ها در ریاضیات به صورت زیرمجموعه هایی از ضرب دکارتی[ ۲] دو یا چند مجموعهٔ مشابه یا متمایز تعریف می شوند. این رابطه ها می توانند خواص و ویژگی های گوناگونی داشته باشند؛ اما ۴ ویژگی از سایر ویژگی ها مهم تر است. رابطه هایی که این خواص را دارند، به این شکل نامیده می شوند:
• بازتابی[ ۳]
• تقارنی[ ۴]
• پادتقارنی
• ترایایی
رابطه ای که بازتابی، تقارنی و ترایایی باشد، رابطهٔ هم ارزی[ ۵] و رابطه ای که بازتابی، پادتقارنی و ترایایی باشد، رابطهٔ ترتیب[ ۶] خوانده می شود.
• رابطهٔ توازی خطوط در صفحه ( || ) : مثالی از رابطهٔ هم ارزی
نشان می دهیم که رابطهٔ توازی خطوط در صفحه، یک رابطهٔ هم ارزی است:
نخست - هر خط با خودش موازی است؛ پس این رابطه بازتابی است.
دوم - اگر خطی با خط دیگری موازی باشد، آن خط نیز با این خط موازی است؛ پس این رابطه تقارنی است.
سوم - اگر خط d با خط 'd، و خط 'd با خط «d موازی باشند، آن گاه بنابر قضایای هندسهٔ اقلیدسی، خط d با خط»d موازی خواهد بود؛ پس این رابطه ترایایی نیز هست.
به این ترتیب مشخص شد که رابطهٔ توازی، یک رابطهٔ هم ارزی است.
• رابطهٔ بزرگ تر مساوی بودن ( ≥ {\displaystyle \geq } ) : مثالی از رابطهٔ ترتیب
نشان می دهیم که رابطهٔ ≥ یک رابطهٔ ترتیب است:
نخست - هر عدد از خودش بزرگ تر یا با خودش مساوی است؛ پس این رابطه بازتابی است.
دوم - اگر a ≥ b و b ≥ a آن گاه نتیجه می شود که a = b ؛ پس این رابطه پادتقارنی است.
سوم - اگر a ≥ b و b ≥ c آن گاه نتیجه می شود که a ≥ c ؛ پس این رابطه ترایایی است.
به این ترتیب مشخص شد که رابطهٔ ≥ یک رابطهٔ ترتیب است.
وقتی یک رابطهٔ هم ارزی را روی مجموعه ای تعریف می کنیم، این رابطه مجموعه را به دسته ( کلاس ) های هم ارزی[ ۷] افراز می کند. به عنوان نمونه، همان مثال توازی خطوط را در نظر بگیرید. این رابطه، رابطه ای هم ارزی است و خطوط موجود در صفحه را به دسته های هم ارزی افراز می کند؛ به طوری که همهٔ خطوط موجود در هر دسته، با هم موازی اند.
یک مثال مفید دیگر برای درک بهتر دسته های هم ارزی، رابطهٔ هم باقی ماندگی اعداد طبیعی به پیمانه ای مشخص[ ۸] است. نشان دادن این که این رابطه هم ارزی ست، بسیار ساده است و لذا از اثبات آن می گذریم. به این ترتیب همان طور که گفته شد، این رابطه مجموعهٔ اعداد طبیعی را به دسته های هم ارزی افراز خواهد کرد. اعداد موجود در هریک از این دسته ها، به پیمانهٔ m باقی ماندهٔ یکسانی خواهند داشت.




wiki: رابطه هم ارزی
