در ریاضیات، رابطهٔ بازتابی[ ۱] ( به انگلیسی: Reflexive relation ) رابطه ای است که برای یک مجموعهٔ ناتُهی تعریف می شود و به رابطهٔ دوتایی ای می گویند که همهٔ عناصر مجموعه آن رابطه را با خودشان داشته باشند. [ ۲]
هر رابطهٔ همانی یک رابطهٔ بازتابی است با این حال هر رابطهٔ بازتابی لزوماً همانی نیست. [ ۳]
اگر A = { 1 , 2 , 3 } و رابطهٔ دوتایی R 1 به صورت R 1 = { ( 1 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 3 ) } تعریف شود، آنگاه R 1 یک رابطهٔ بازتابی خواهد بود. ولی رابطهٔ R 2 = { ( 1 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 2 ) } بازتابی نیست زیرا با وجود اینکه 3 ∈ A ، اما ( 3 , 3 ) ∉ R 2 . [ ۴]
ماتریس متناظر با رابطه ی بازتابی، ماتریسی است که همه ی درایه های قطر اصلی آن یک باشد. بنابرین ماتریس M = با n سطر و n ستون دارای خاصیت بازتابی است اگر:
ماتریس M 1 = دارای خاصیت بازتابی است زیرا تمام درایه های قطر اصلی آن یک هستند. ولی ماتریس M 2 = دارای خاصیت بازتابی نیست زیرا تمام درایه های قطر اصلی آن یک نیستند.
گراف متناظر با رابطه ی بازتابی، گرافی است که تمام رئوس آن دارای حلقه ( loop ) باشد.
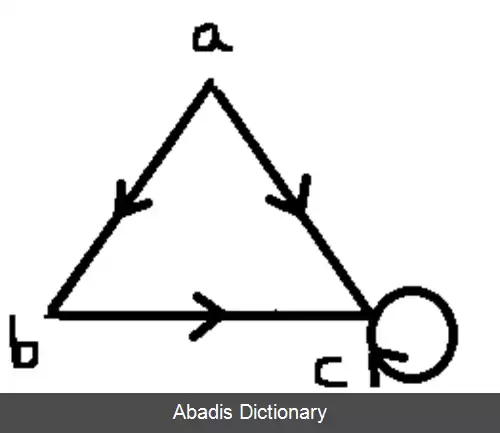
تصویر 1 نشان دهنده ی گرافی است که دارای خاصیت بازتابی است زیرا تمام رئوس آن دارای حلقه است . و تصویر 2 نشان دهنده ی گرافی است که خاصیت بازتابی ندارد زیرا رئوس a, b آن دارای حلقه نمی باشند.
اگر رابطه R دارای خاصیت بازتابی نباشد رابطه ی R ′ که شامل R بوده و خاصیت بازتابی نیز دارد و زیر مجموعه ی هر رابطه ی دیگری که شامل R است نیز باشد بستار بازتابی رابطه ی R نامیده می شود.
همانطور که در مثال 1 دیدید رابطهٔ R 2 = { ( 1 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 2 ) } بازتابی نیست. حال اگر زوج مرتب ( 3 , 3 ) را به رابطه ی R 2 بیفزاییم رابطه ی R 2 ′ = { ( 1 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 2 ) , ( 3 , 3 ) } بدست می آید که همان بستار بازتابی رابطه ی R 2 نامیده می شود.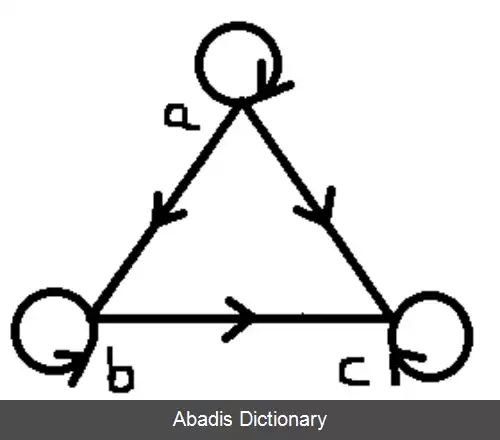
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهر رابطهٔ همانی یک رابطهٔ بازتابی است با این حال هر رابطهٔ بازتابی لزوماً همانی نیست. [ ۳]
اگر A = { 1 , 2 , 3 } و رابطهٔ دوتایی R 1 به صورت R 1 = { ( 1 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 3 ) } تعریف شود، آنگاه R 1 یک رابطهٔ بازتابی خواهد بود. ولی رابطهٔ R 2 = { ( 1 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 2 ) } بازتابی نیست زیرا با وجود اینکه 3 ∈ A ، اما ( 3 , 3 ) ∉ R 2 . [ ۴]
ماتریس متناظر با رابطه ی بازتابی، ماتریسی است که همه ی درایه های قطر اصلی آن یک باشد. بنابرین ماتریس M = با n سطر و n ستون دارای خاصیت بازتابی است اگر:
ماتریس M 1 = دارای خاصیت بازتابی است زیرا تمام درایه های قطر اصلی آن یک هستند. ولی ماتریس M 2 = دارای خاصیت بازتابی نیست زیرا تمام درایه های قطر اصلی آن یک نیستند.
گراف متناظر با رابطه ی بازتابی، گرافی است که تمام رئوس آن دارای حلقه ( loop ) باشد.
تصویر 1 نشان دهنده ی گرافی است که دارای خاصیت بازتابی است زیرا تمام رئوس آن دارای حلقه است . و تصویر 2 نشان دهنده ی گرافی است که خاصیت بازتابی ندارد زیرا رئوس a, b آن دارای حلقه نمی باشند.
اگر رابطه R دارای خاصیت بازتابی نباشد رابطه ی R ′ که شامل R بوده و خاصیت بازتابی نیز دارد و زیر مجموعه ی هر رابطه ی دیگری که شامل R است نیز باشد بستار بازتابی رابطه ی R نامیده می شود.
همانطور که در مثال 1 دیدید رابطهٔ R 2 = { ( 1 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 2 ) } بازتابی نیست. حال اگر زوج مرتب ( 3 , 3 ) را به رابطه ی R 2 بیفزاییم رابطه ی R 2 ′ = { ( 1 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 2 ) , ( 3 , 3 ) } بدست می آید که همان بستار بازتابی رابطه ی R 2 نامیده می شود.


wiki: رابطه بازتابی
