در نظریه گراف دور اویلری یا مدار اویلری ( به انگلیسی: Eulerian circuit ) به مسیری گفته می شود که از یک رأس شروع شود و از تمامی یال ها یکبار ( و فقط یکبار ) بگذرد و به همان رأس بازگردد. اگر مسیر از تمام یال ها عبور کند ولی به جای اولش بازنگردد به آن مسیر اویلری ( به انگلیسی: Eulerian path ) می گویند.
دور اویلری زمانی وجود دارد که گراف همبند باشد و درجه هر رأس زوج باشد، یعنی تعداد یال های متصل به آن عددی زوج باشد. به یک گراف، گراف اویلری گفته می شود اگر و فقط اگر گراف همبند باشد و درجه تمام رأس های آن زوج باشد. ( با فرض اینکه مؤلفه بدیهی نداشته باشیم ) [ ۱]
مسیرهای اویلری در بیوانفورماتیک برای بازسازی توالی دی ان ای ( توالی اسید نوکلئیک ) از قطعات آن مورد استفاده قرار میگیرد. [ ۲] مسیرهای اویلری همچنین در طراحی مدار CMOS برای پیدا کردن ترتیب دروازه منطقی بهینه مورد استفاده قرار می گیرند. [ ۳] مضاف بر این الگوریتم های متعددی برای پردازش درخت ها وجود دارد که از دورهای اویلری استفاده می کنند. [ ۴] [ ۵]
مک کِی و رابینسون اثبات کردند که تعدادِ دورهای اویلری در گرافهای کامل به فرمول پایین میل می کند:[ ۶]
بعدها ایزائف اثبات کرد تعداد دورهای اویلری در گرافهای کامل دو بخشی به صورت مجانبی برابر است با:[ ۷]
الگوریتم پیدا کردن مدار اویلری: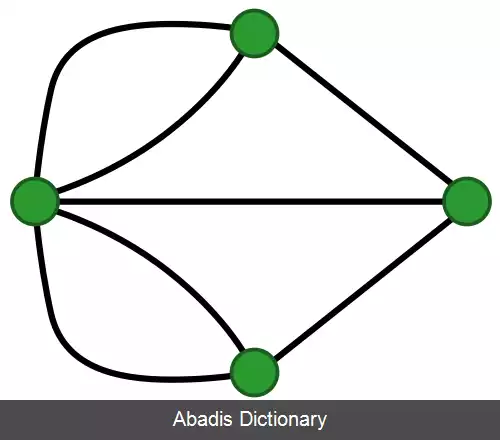
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدور اویلری زمانی وجود دارد که گراف همبند باشد و درجه هر رأس زوج باشد، یعنی تعداد یال های متصل به آن عددی زوج باشد. به یک گراف، گراف اویلری گفته می شود اگر و فقط اگر گراف همبند باشد و درجه تمام رأس های آن زوج باشد. ( با فرض اینکه مؤلفه بدیهی نداشته باشیم ) [ ۱]
مسیرهای اویلری در بیوانفورماتیک برای بازسازی توالی دی ان ای ( توالی اسید نوکلئیک ) از قطعات آن مورد استفاده قرار میگیرد. [ ۲] مسیرهای اویلری همچنین در طراحی مدار CMOS برای پیدا کردن ترتیب دروازه منطقی بهینه مورد استفاده قرار می گیرند. [ ۳] مضاف بر این الگوریتم های متعددی برای پردازش درخت ها وجود دارد که از دورهای اویلری استفاده می کنند. [ ۴] [ ۵]
مک کِی و رابینسون اثبات کردند که تعدادِ دورهای اویلری در گرافهای کامل به فرمول پایین میل می کند:[ ۶]
بعدها ایزائف اثبات کرد تعداد دورهای اویلری در گرافهای کامل دو بخشی به صورت مجانبی برابر است با:[ ۷]
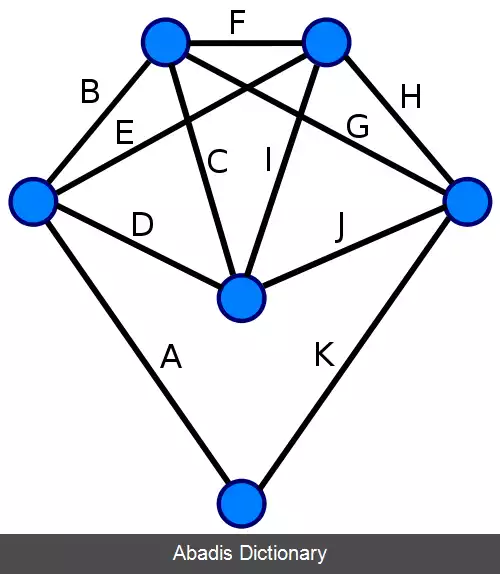
الگوریتم پیدا کردن مدار اویلری:


wiki: دور اویلری
