دنباله دقیق ( به انگلیسی: Exact Sequence ) مفهومی در ریاضیات، بخصوص در نظریه گروه ها، نظریه حلقه ها، نظریه مدول ها، جبر همولوژی و همچنین در هندسه دیفرانسیل است. یک دنباله دقیق، دنباله ای است که شامل تعدادی متناهی یا نامتناهی از اشیاء و ریخت های بین آن هاست، به گونه ای که تصویر یک ریخت برابر هسته ریخت بعدیست.
در نظریه گروه ها، یک دنباله از گروه ها و همریختی ها به شکل:
را در دقیق گوییم اگر im ( f i ) = ker ( f i + 1 ) . همچنین دنباله را یک دنباله دقیق گوییم هرگاه به ازای هر 1 ≤ i < n در دقیق باشد.
دنباله گروه ها و همریختی های گروهی ممکن است متناهی یا نامتناهی باشد.
برای ساختارهای جبری دیگر نیز می توان تعریف مشابهی ارائه کرد. به عنوان مثال می توان دنبال دقیقی از فضاهای برداری و نگاشت خطی بینشان، یا مدول ها و همریختی های مدولی بین آن ها ایجاد کرد. به طور کلی، مفهوم دنباله دقیق در هر رسته ای که دارای هسته و هم - هسته باشد قابل پیاده سازیست.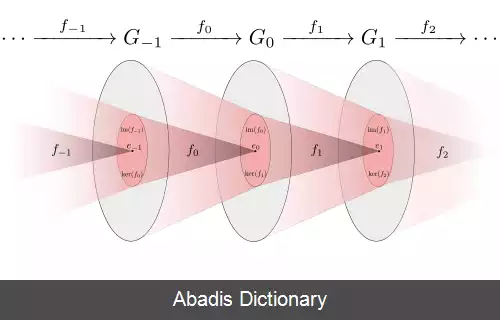
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر نظریه گروه ها، یک دنباله از گروه ها و همریختی ها به شکل:
را در دقیق گوییم اگر im ( f i ) = ker ( f i + 1 ) . همچنین دنباله را یک دنباله دقیق گوییم هرگاه به ازای هر 1 ≤ i < n در دقیق باشد.
دنباله گروه ها و همریختی های گروهی ممکن است متناهی یا نامتناهی باشد.
برای ساختارهای جبری دیگر نیز می توان تعریف مشابهی ارائه کرد. به عنوان مثال می توان دنبال دقیقی از فضاهای برداری و نگاشت خطی بینشان، یا مدول ها و همریختی های مدولی بین آن ها ایجاد کرد. به طور کلی، مفهوم دنباله دقیق در هر رسته ای که دارای هسته و هم - هسته باشد قابل پیاده سازیست.

wiki: دنباله دقیق
