دستگاه مختصات استوانه ای ( به انگلیسی: cylindrical coordinate system ) نوعی از دستگاه مختصات سه بعدی است که در آن یک نقطه در فضا، بر روی سطح یک استوانه فرضی در نظر گرفته می شود. مختصات یا مکان آن نقطه بر اساس فاصله آن از محور عمودی ( شعاع استوانه ) ، فاصله نقطه از قاعده ( ارتفاع استوانه ) و زاویه ای که شعاع قاعده گذرنده از آن نقطه با محور می سازد ، بیان می شود. هر چند علامت ها یا حروف تعیین شده استاندارد برای این دستگاه ( , , ) هستند ولی با این حال در برخی های شاخه های مهندسی به ترتیب از حروف r, θ, استفاده می شود.
مبدأ دستگاه مختصات استوانه ای نقطه ای است که هر سه مختصات را می توان صفر در نظر گرفت.
دستگاه مختصات استوانه ای در حالت دوبعدی، با حذف مختص به مختصات قطبی تبدیل می شود.
ممکن است معادله یک رویه در یکی از دستگاه های ساده تر از معادله آن در دستگاه دکارتی باشد. در چنین مواردی استفاده از دستگاه مناسب باعث صرفه جویی در وقت می شود. این موضوع در حل انتگرال های چندگانه اهمیت بیشتری پیدا می کند. همان طور که می دانید حل برخی انتگرال های سه گانه در دستگاه دکارتی گاهی غیرممکن می باشد، ولی با یک تغییر مختصات ساده به راحتی می توانیم به جواب مورد نظر برسیم. در دستگاه مختصات استوانه ای، استوانه هایی که محورشان در امتداد محور z هستند معادلات بسیار ساده ای دارند. این دستگاه مختصات در فضا از طریق تلفیق مختصات قطبی در صفحه xy با محور z معمولی به دست می آید. به این ترتیب به هر نقطه در فضا یک یا چند سه تایی مختصات به صورت ( r، θ، z ) نسبت داده می شود. در فیزیک و به ویژه در مباحث الکترومغناطیس و مخابرات به جای r، θ، z به ترتیب از حروف ρ، φ، z استفاده می شود.
در واقع توسط روابط فوق می توان یک نقطه در دستگاه مختصات دکارتی را به دستگاه مختصات استوانه ای منتقل کرد. در مختصات استوانه ای معادله r=a فقط دایره ای در صفحه xy را مشخص نمی کند بلکه استوانه ای کامل حول محور z را توصیف می کند. خود محور z با معادله r=0 معین می شود. معادله θ=θ۰ توصیف کننده صفحه ای است که شامل محور z است و زاویه ای به اندازه θ۰ رادیان با قسمت مثبت محور x می سازد. چند رابطه که مختصات دکارتی، استوانه ای و کروی را به هم مربوط می سازند.
• "Cylinder coordinates", Encyclopedia of Mathematics, EMS Press, 2001
• توضیحات مث ورلد از دستگاه مختصات استوانه ای
• انیمیشن محورهای مختصات استوانه ای توسط فرانک واتنبرگ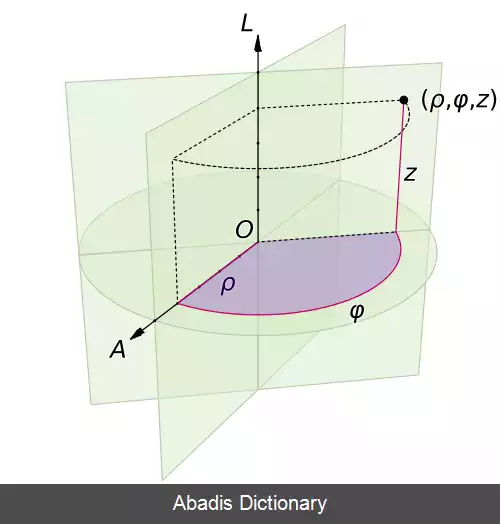
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمبدأ دستگاه مختصات استوانه ای نقطه ای است که هر سه مختصات را می توان صفر در نظر گرفت.
دستگاه مختصات استوانه ای در حالت دوبعدی، با حذف مختص به مختصات قطبی تبدیل می شود.
ممکن است معادله یک رویه در یکی از دستگاه های ساده تر از معادله آن در دستگاه دکارتی باشد. در چنین مواردی استفاده از دستگاه مناسب باعث صرفه جویی در وقت می شود. این موضوع در حل انتگرال های چندگانه اهمیت بیشتری پیدا می کند. همان طور که می دانید حل برخی انتگرال های سه گانه در دستگاه دکارتی گاهی غیرممکن می باشد، ولی با یک تغییر مختصات ساده به راحتی می توانیم به جواب مورد نظر برسیم. در دستگاه مختصات استوانه ای، استوانه هایی که محورشان در امتداد محور z هستند معادلات بسیار ساده ای دارند. این دستگاه مختصات در فضا از طریق تلفیق مختصات قطبی در صفحه xy با محور z معمولی به دست می آید. به این ترتیب به هر نقطه در فضا یک یا چند سه تایی مختصات به صورت ( r، θ، z ) نسبت داده می شود. در فیزیک و به ویژه در مباحث الکترومغناطیس و مخابرات به جای r، θ، z به ترتیب از حروف ρ، φ، z استفاده می شود.
در واقع توسط روابط فوق می توان یک نقطه در دستگاه مختصات دکارتی را به دستگاه مختصات استوانه ای منتقل کرد. در مختصات استوانه ای معادله r=a فقط دایره ای در صفحه xy را مشخص نمی کند بلکه استوانه ای کامل حول محور z را توصیف می کند. خود محور z با معادله r=0 معین می شود. معادله θ=θ۰ توصیف کننده صفحه ای است که شامل محور z است و زاویه ای به اندازه θ۰ رادیان با قسمت مثبت محور x می سازد. چند رابطه که مختصات دکارتی، استوانه ای و کروی را به هم مربوط می سازند.
• "Cylinder coordinates", Encyclopedia of Mathematics, EMS Press, 2001
• توضیحات مث ورلد از دستگاه مختصات استوانه ای
• انیمیشن محورهای مختصات استوانه ای توسط فرانک واتنبرگ

wiki: دستگاه مختصات استوانه ای
