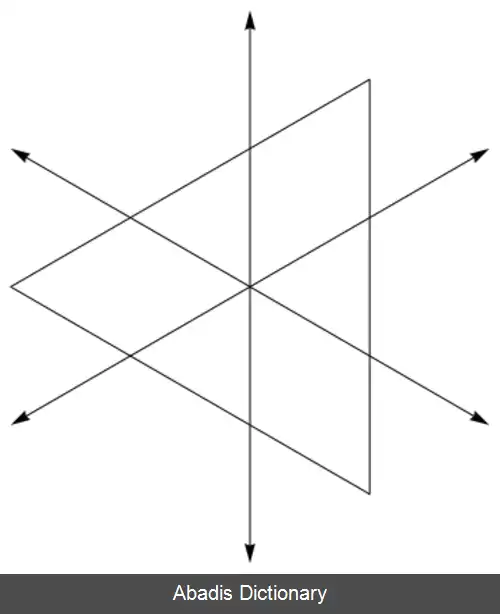
دستگاه ریشه ای

دستگاه ریشه ای ( به انگلیسی: Root System ) ، پیکره بندی از بردارها در فضای اقلیدسی است که در خواص هندسی به خصوصی صدق می کنند. این مفهوم در نظریه گروه های لی و جبرهای لی، به خصوص در رده بندی و نظریه نمایش مربوط به جبرهای لی نیم - ساده، نقش بنیادینی دارد. از آنجا که گروه های لی ( و برخی از اشیاء مشابه آن ها چون گروه های جبری ) و جبرهای لی، طی قرن بیستم در بسیاری از بخش های ریاضیات نقش مهمی پیدا کرده است. تعدد کاربردهای دستگاه های ریشه ای در حوزه های مختلفی از ریاضیات، نشان دهنده اهمیت ذاتی آن است. همچنین، الگوی رده بندی دستگاه های ریشه ای توسط نمودارهای دینکین، در بخشی از ریاضیات رخ می دهند که لزوماً ارتباط آشکاری با نظریه لی ندارد ( همچون نظریه تکینگی ) . در نهایت، دستگاه های ریشه ای به خودی خود در مواردی چون نظریه طیفی گراف ها، مهم تلقی می گردند. [ ۱]
↑ Cvetković, Dragoš ( 2002 ) . "Graphs with least eigenvalue −2; a historical survey and recent developments in maximal exceptional graphs". Linear Algebra and Its Applications. 356 ( 1–3 ) : 189–210. doi:10. 1016/S0024 - 3795 ( 02 ) 00377 - 4.
• مشارکت کنندگان ویکی پدیا. «Root System». در دانشنامهٔ ویکی پدیای انگلیسی، بازبینی شده در ۲۰ مهٔ ۲۰۲۱.