درهم سازی قابل گسترش نوعی سامانه[ ۱] درهم سازی پویا است که با خروجی تابع درهم سازی مانند یک رشته بیتی ( نمایش دودویی آن ) رفتار می کند و از یک درخت پیشوندی برای جستجوی سطل استفاده می کند. [ ۲] به دلیل سلسله مراتبی[ ۳] بودن سامانه، درهم سازی دوباره یک عمل افزایشی است ( در صورت نیاز، هر بار یک سطل تکمیل می شود ) . این بدان معنی است که برنامه های حساس به زمان، از رشد جدول، کمتر از درهم سازی دوبارهٔ تمام جدول تحت تأثیر قرار می گیرند.
درهم سازی قابل گسترش اولین بار توسط رونالد فاگین در سال ۱۹۷۹ توصیف شد. عملاً همه سامانه های پرونده مدرن از درهم سازی قابل گسترش یا درختان B استفاده می کنند. به طور خاص، سامانه پرونده جهانی، ZFS و سیستم فایل های SpadFS از درهم سازی قابل گسترش استفاده می کنند. [ ۴]
فرض کنید که تابع درهم سازی h ( k ) رشته ای از بیت ها را برگرداند. اولین i بیت هر رشته به عنوان اندیس هایی استفاده می شوند تا مشخص شود که آنها در کجای جدول درهم سازی قرار خواهند گرفت. علاوه بر این، i کوچکترین عددی است؛ به طوری که اندیس هر عنصر در جدول یکتا است.
فرض کنید درهم سازی سه کلید k 1 , k 2 , k 3 بصورت زیر باشد:
فرض کنیم که برای این مثال خاص، اندازه سطل ۱ است و k 1 , k 2 ، دو کلیدی هستند که باید اول درج شوند. این دو کلید می توانند بر اساس با ارزش ترین بیت تفکیک شوند و به شرح زیر در جدول قرار گیرند:
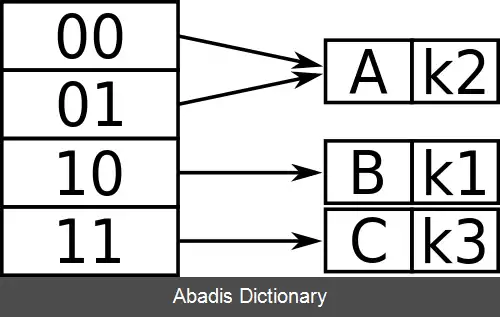
حال، اگر قرار باشد که k 3 در جدول درهم سازی شود، برای تشخیص هر سه کلید تنها یک بیت کافی نیست ( زیرا در نمایش بیتی k 1 , k 3 چپ ترین بیت ۱ است ) . همچنین، چون اندازه سطل یک است، جدول سرریز می شود. از آنجا که مقایسه بر اساس دو بیت اول، به هر کلید یک مکان یکتا نسبت می دهد، اندازه فهرست به شرح زیر دو برابر می شود:
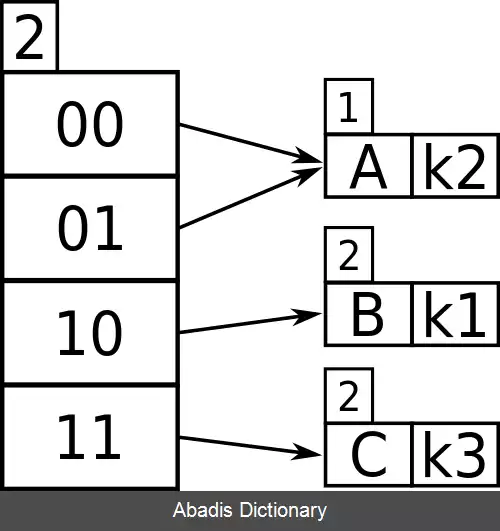
بنابراین، اکنون k 1 , k 3 دارای موقعیتی یکتا هستند که با دو بیت چپ متمایز می شوند. از آنجا که k 2 در نیمه بالای جدول است، ۰۰ و ۰۱ هر دو به آن اشاره دارند زیرا هیچ کلید دیگری برای مقایسه با آن وجود ندارد که با ۰ شروع شود.
مثال بالا از ( Fagin و دیگران 1979 ) .
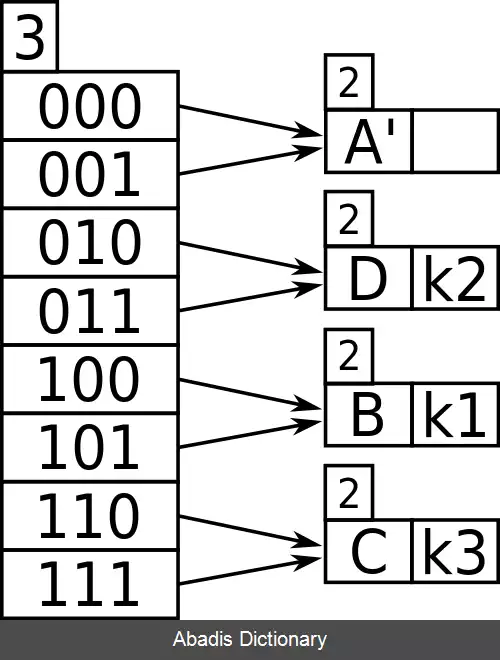
فرض کنید:
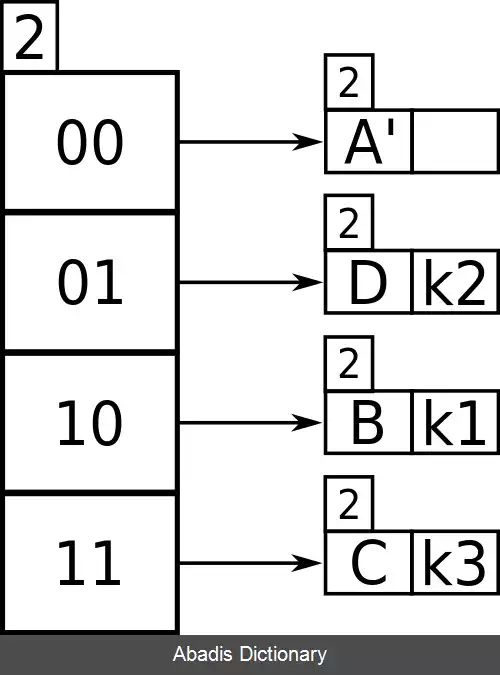
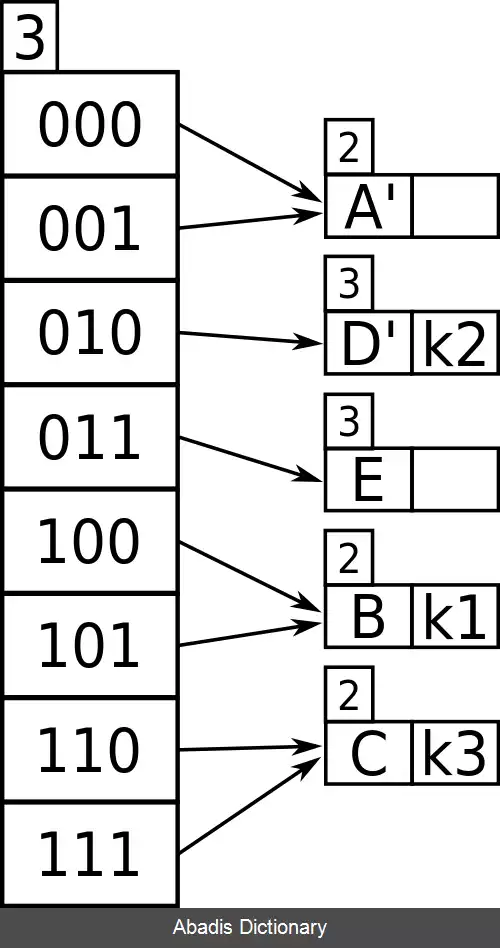
حال k 4 باید درج شود، و دو بیت اول آن به شکل ۰۱ هستند، و با استفاده از عمق ۲ بیت در جدول، از ۰۱ به سطل A نگاشته می شود. سطل A پر است ( حداکثر اندازه ۱ است ) ، بنابراین باید تقسیم شود؛ از آنجا که بیش از یک اشاره گر به سطل A وجود دارد، نیازی به افزایش اندازه جدول نیست.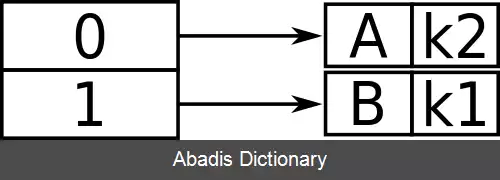
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدرهم سازی قابل گسترش اولین بار توسط رونالد فاگین در سال ۱۹۷۹ توصیف شد. عملاً همه سامانه های پرونده مدرن از درهم سازی قابل گسترش یا درختان B استفاده می کنند. به طور خاص، سامانه پرونده جهانی، ZFS و سیستم فایل های SpadFS از درهم سازی قابل گسترش استفاده می کنند. [ ۴]
فرض کنید که تابع درهم سازی h ( k ) رشته ای از بیت ها را برگرداند. اولین i بیت هر رشته به عنوان اندیس هایی استفاده می شوند تا مشخص شود که آنها در کجای جدول درهم سازی قرار خواهند گرفت. علاوه بر این، i کوچکترین عددی است؛ به طوری که اندیس هر عنصر در جدول یکتا است.
فرض کنید درهم سازی سه کلید k 1 , k 2 , k 3 بصورت زیر باشد:
فرض کنیم که برای این مثال خاص، اندازه سطل ۱ است و k 1 , k 2 ، دو کلیدی هستند که باید اول درج شوند. این دو کلید می توانند بر اساس با ارزش ترین بیت تفکیک شوند و به شرح زیر در جدول قرار گیرند:
حال، اگر قرار باشد که k 3 در جدول درهم سازی شود، برای تشخیص هر سه کلید تنها یک بیت کافی نیست ( زیرا در نمایش بیتی k 1 , k 3 چپ ترین بیت ۱ است ) . همچنین، چون اندازه سطل یک است، جدول سرریز می شود. از آنجا که مقایسه بر اساس دو بیت اول، به هر کلید یک مکان یکتا نسبت می دهد، اندازه فهرست به شرح زیر دو برابر می شود:
بنابراین، اکنون k 1 , k 3 دارای موقعیتی یکتا هستند که با دو بیت چپ متمایز می شوند. از آنجا که k 2 در نیمه بالای جدول است، ۰۰ و ۰۱ هر دو به آن اشاره دارند زیرا هیچ کلید دیگری برای مقایسه با آن وجود ندارد که با ۰ شروع شود.
مثال بالا از ( Fagin و دیگران 1979 ) .
فرض کنید:
حال k 4 باید درج شود، و دو بیت اول آن به شکل ۰۱ هستند، و با استفاده از عمق ۲ بیت در جدول، از ۰۱ به سطل A نگاشته می شود. سطل A پر است ( حداکثر اندازه ۱ است ) ، بنابراین باید تقسیم شود؛ از آنجا که بیش از یک اشاره گر به سطل A وجود دارد، نیازی به افزایش اندازه جدول نیست.






wiki: درهم سازی قابل گسترش
