درهم سازی دوگانه یک تکنیک برنامه نویسی کامپیوتر است که در جدول های درهم سازی برای رفع برخورد در درهم سازی؛ نمونه هایی که وقتی دو مقدار مختلف برای تولید یک کلید درهمسازی یکسان جستجو می شوند؛
این یک تکنیک محبوب رفع برخورد در جدول های درهمسازی آدرس باز است. درهمسازی دوگانه در کتابخانه های محبوب زیادی پیاده سازی شده است.
همچون جستجوی خطی، از یک مقدار درهم سازی به عنوان نقطه شروع استفاده می کند و سپس مکرراً یک بازه را پشت سر می گذارد تا مقدار مورد نظر را مکان یابی شود؛ یا به یک مکان تهی برسد یا تمامی جدول جستجو شده باشد؛ اما در این حالت این بازه از یک تابع مستقل درهمسازی دیگری استفاده می کند. ( به همین دلیل اسم این تکنیک درهمسازی دوگانه است. )
برخلاف جستجوی خطی و جستجوی درجه ی دوم، بازه به داده وابسته است. به همین دلیل مقادیر یکسانی به یک مکان یکسان نگاشته می شوند ولی دارای دنباله های متفاوتی هستند. این برخوردهای مکرر و تأثیر بربروی بازه ها را کمینه می کند.
دو تابع درهم سازی تصادفی، یکنواخت، مستقل و انتخاب شدهٔ h_1, h_2 داده شده است. مکان i - ام در طول دنباله برای مقدار k در یک جدول ترکیبی T به صورت
h ( i , k ) = ( h 1 ( k ) + i h 2 ( k ) ) است. به طور کلی این دو تابع از یک مجموعه توابع درهمسازی جهانی انتخاب می شوند.
درهم سازی دوگانه با آدرس باز، یک ساختار داده کلاسیک برای جدول T می باشد. n را تعداد اعضای ذخیره شده در T در نظر بگیرید در این صورت ضریب بار برابر است با
( |α= n/ ( |T
درهم سازی دوگانه، آدرس های باز یکنوای درهم سازی را تخمین می زند. بدین صورت که دو تابع درهم سازی جهانی مانند h_2 و h_1 را تصادفی، یکنواخت و مستقل انتخاب می کنیم تا جدول درهمسازی دوگانه T آن ها را ایجاد کنیم. تمام عناصر به وسیله درهم سازی دوگانه با استفاده از توابع h_2 و h_1 در جدول T قرارداده می شوند. برای k مورد نظر، مکان ( i+1 ) ام مورد نظر ار طریق فرمول زیر محاسبه می شود.
h ( i , k ) = ( h 1 ( k ) + i . h 2 ( k ) ) m o d e | T |
T را با یک ضریب بار داده شدهٔ α بین 0 و 1 در نظر بگیرید. بردفورد و کیتاکس یک مقدار برای تعداد جستجوی های ناموفق در جدول T بدون در نظر داشتن توزیع ورودی به دست آوردند که تقریباً 1/ ( 1 - α ) است. دقیقتر، این دو تابع درهم سازی تصادفی، یکنواخت و مستقل انتخاب شده از یک مجموعه توابع ترکیبی جهانی که دو به دو مستقل هستند، انتخاب شده اند. همچنین این نتیجه به دست آمده شامل نتیجهٔ گبیس و سموردی می شود که نشان دادند مقدار خطای به دست آمده برای ضریب بار α< 0. 319 برابر 1/ ( 1 - α ) است. همچنین لوکر و مولودویچ هم چنین نتایجی را به دست آوردند. اثمیت و سیگل این مقدار را برای توابع مستقل و یکنواخت k=C logn با ضریب ثابت C به دست آوردند.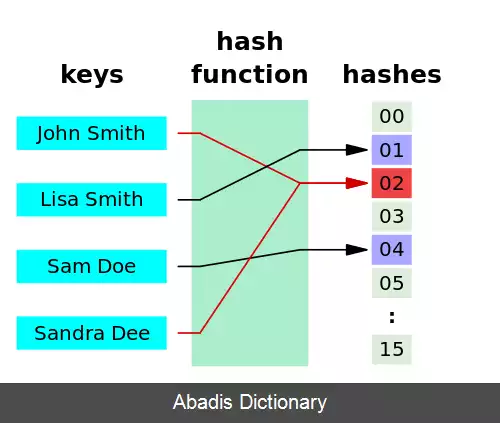
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین یک تکنیک محبوب رفع برخورد در جدول های درهمسازی آدرس باز است. درهمسازی دوگانه در کتابخانه های محبوب زیادی پیاده سازی شده است.
همچون جستجوی خطی، از یک مقدار درهم سازی به عنوان نقطه شروع استفاده می کند و سپس مکرراً یک بازه را پشت سر می گذارد تا مقدار مورد نظر را مکان یابی شود؛ یا به یک مکان تهی برسد یا تمامی جدول جستجو شده باشد؛ اما در این حالت این بازه از یک تابع مستقل درهمسازی دیگری استفاده می کند. ( به همین دلیل اسم این تکنیک درهمسازی دوگانه است. )
برخلاف جستجوی خطی و جستجوی درجه ی دوم، بازه به داده وابسته است. به همین دلیل مقادیر یکسانی به یک مکان یکسان نگاشته می شوند ولی دارای دنباله های متفاوتی هستند. این برخوردهای مکرر و تأثیر بربروی بازه ها را کمینه می کند.
دو تابع درهم سازی تصادفی، یکنواخت، مستقل و انتخاب شدهٔ h_1, h_2 داده شده است. مکان i - ام در طول دنباله برای مقدار k در یک جدول ترکیبی T به صورت
h ( i , k ) = ( h 1 ( k ) + i h 2 ( k ) ) است. به طور کلی این دو تابع از یک مجموعه توابع درهمسازی جهانی انتخاب می شوند.
درهم سازی دوگانه با آدرس باز، یک ساختار داده کلاسیک برای جدول T می باشد. n را تعداد اعضای ذخیره شده در T در نظر بگیرید در این صورت ضریب بار برابر است با
( |α= n/ ( |T
درهم سازی دوگانه، آدرس های باز یکنوای درهم سازی را تخمین می زند. بدین صورت که دو تابع درهم سازی جهانی مانند h_2 و h_1 را تصادفی، یکنواخت و مستقل انتخاب می کنیم تا جدول درهمسازی دوگانه T آن ها را ایجاد کنیم. تمام عناصر به وسیله درهم سازی دوگانه با استفاده از توابع h_2 و h_1 در جدول T قرارداده می شوند. برای k مورد نظر، مکان ( i+1 ) ام مورد نظر ار طریق فرمول زیر محاسبه می شود.
h ( i , k ) = ( h 1 ( k ) + i . h 2 ( k ) ) m o d e | T |
T را با یک ضریب بار داده شدهٔ α بین 0 و 1 در نظر بگیرید. بردفورد و کیتاکس یک مقدار برای تعداد جستجوی های ناموفق در جدول T بدون در نظر داشتن توزیع ورودی به دست آوردند که تقریباً 1/ ( 1 - α ) است. دقیقتر، این دو تابع درهم سازی تصادفی، یکنواخت و مستقل انتخاب شده از یک مجموعه توابع ترکیبی جهانی که دو به دو مستقل هستند، انتخاب شده اند. همچنین این نتیجه به دست آمده شامل نتیجهٔ گبیس و سموردی می شود که نشان دادند مقدار خطای به دست آمده برای ضریب بار α< 0. 319 برابر 1/ ( 1 - α ) است. همچنین لوکر و مولودویچ هم چنین نتایجی را به دست آوردند. اثمیت و سیگل این مقدار را برای توابع مستقل و یکنواخت k=C logn با ضریب ثابت C به دست آوردند.

wiki: درهم سازی دوگانه
