درخت 2 - 3 - 4
در علوم کامپیوتر، درخت 2 - 3 - 4 ( که به آن درخت 2 - 4 هم گفته می شود ) داده ساختاری است که عموماً برای پیاده سازی فهرست ها ( لیست ها ) استفاده می شوند. عدد هر گره نشانگر تعداد فرزندان گره است که می تواند دو، سه یا چهار گره باشند :
• گره - 2، یک مقدار و دو گره فرزند دارد
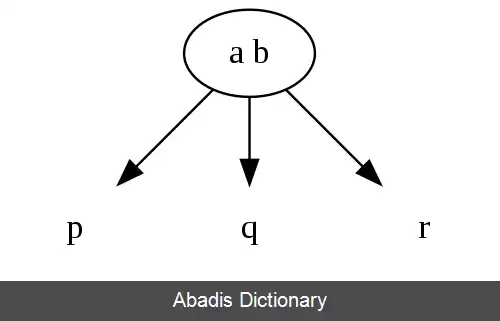
• گره - 3، دو مقدار و سه گره فرزند دارد
• گره - 4، سه مقدار و چهار گره فرزند دارد
درختهای 2 - 3 - 4 درخت باینری مرتبه 4 هستند و مانند درخت باینری می توانند عملیات جستجو، درج کردن و حذف کردن را در زمان ( O ( log n انجام دهند. یک خاصیت این درخت این است که تمامی برگ ها ( پایین ترین گره که فرزند هم ندارد ) در یک ارتفاع هستند . درخت های 2 - 3 - 4 و درخت های قرمز - سیاه یک به یک هستند، به این معنا که برای هر درخت 2 - 3 - 4 فقط یک درخت قرمز - سیاه وجود دارد . عملیات درج کردن و حذف کردن روی درخت 2 - 3 - 4 موجب گسترش، جـدا شدن و ادغام گره ها می شود که معادل تعویض رنگ و جابجایی گره ها در درخت قـرمز - سیاه است . برای آشنایی با درخت قـرمز - سیاه معــمولا در ابتــدا درخت 2 - 3 - 4 معرفی می شود، چرا که در مفهوم آسانتر است. اما بدلیل حالتهای خاص در انجام عملیات روی درخت 2 - 3 - 4 پیاده سازی این درخت در بسیاری از زبانهای برنامه نویسی مشکل است. چون پیاده سازی درخت قرمز - سیاه آسانتر است به درخت 2 - 3 - 4 ترجیح داده می شود .
• هر گره، یک گره - 2 یا گره - 3 یا گره - 4 است که به ترتیب شامل یک، دو، سه مقدار می شود.
• تمامی برگ ها در یک ارتفاع قرار می گیرند.
• تمامی داده ها ترتیب عددی دارند.
برای درج یک عدد از ریشه شروع می کنیم .
1 . اگر گروه گره - 4 بود :
• مقدار وسط را حذف می کنیم تا تبدیل به گره - 3 شود.
• دو مقدار گره - 3 را در دو گروه جداگانه قرار می دهیم.
• اگر گره مورد نظر ریشه بود :
• مقدار وسط تبدیل ریشه جدید گره - 2 می شود و ارتفاع درخت عدد یک افزوده میشود.
• در غیر این صورت مقدار وسطی ( حذف شده ) به گره پدر منتقل می شود .
2 . فرزندی را پیدا می کنیم که بتواند شامل عدد مورد نظر شود .
3 . اگر فرزند فرزندی نداشت عدد را به همان گره اضافه می کنیم .
• در غیر اینصورت به سراغ فرزند می رویم و همین کار را تکرار می کنیم .
برای حذف کردن یک عنصر از درخت 2 - 3 - 4 1 . عنصر مورد نظر را پیدا می کنیم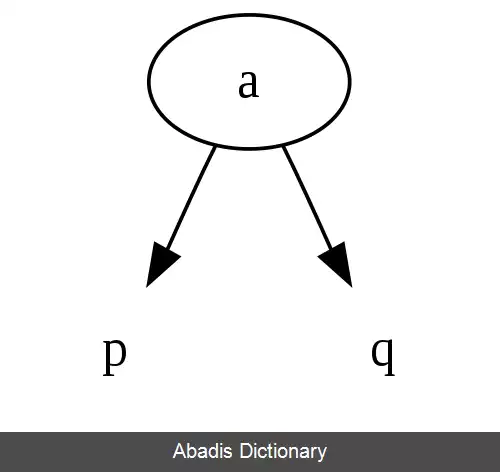
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر علوم کامپیوتر، درخت 2 - 3 - 4 ( که به آن درخت 2 - 4 هم گفته می شود ) داده ساختاری است که عموماً برای پیاده سازی فهرست ها ( لیست ها ) استفاده می شوند. عدد هر گره نشانگر تعداد فرزندان گره است که می تواند دو، سه یا چهار گره باشند :
• گره - 2، یک مقدار و دو گره فرزند دارد
• گره - 3، دو مقدار و سه گره فرزند دارد
• گره - 4، سه مقدار و چهار گره فرزند دارد
درختهای 2 - 3 - 4 درخت باینری مرتبه 4 هستند و مانند درخت باینری می توانند عملیات جستجو، درج کردن و حذف کردن را در زمان ( O ( log n انجام دهند. یک خاصیت این درخت این است که تمامی برگ ها ( پایین ترین گره که فرزند هم ندارد ) در یک ارتفاع هستند . درخت های 2 - 3 - 4 و درخت های قرمز - سیاه یک به یک هستند، به این معنا که برای هر درخت 2 - 3 - 4 فقط یک درخت قرمز - سیاه وجود دارد . عملیات درج کردن و حذف کردن روی درخت 2 - 3 - 4 موجب گسترش، جـدا شدن و ادغام گره ها می شود که معادل تعویض رنگ و جابجایی گره ها در درخت قـرمز - سیاه است . برای آشنایی با درخت قـرمز - سیاه معــمولا در ابتــدا درخت 2 - 3 - 4 معرفی می شود، چرا که در مفهوم آسانتر است. اما بدلیل حالتهای خاص در انجام عملیات روی درخت 2 - 3 - 4 پیاده سازی این درخت در بسیاری از زبانهای برنامه نویسی مشکل است. چون پیاده سازی درخت قرمز - سیاه آسانتر است به درخت 2 - 3 - 4 ترجیح داده می شود .
• هر گره، یک گره - 2 یا گره - 3 یا گره - 4 است که به ترتیب شامل یک، دو، سه مقدار می شود.
• تمامی برگ ها در یک ارتفاع قرار می گیرند.
• تمامی داده ها ترتیب عددی دارند.
برای درج یک عدد از ریشه شروع می کنیم .
1 . اگر گروه گره - 4 بود :
• مقدار وسط را حذف می کنیم تا تبدیل به گره - 3 شود.
• دو مقدار گره - 3 را در دو گروه جداگانه قرار می دهیم.
• اگر گره مورد نظر ریشه بود :
• مقدار وسط تبدیل ریشه جدید گره - 2 می شود و ارتفاع درخت عدد یک افزوده میشود.
• در غیر این صورت مقدار وسطی ( حذف شده ) به گره پدر منتقل می شود .
2 . فرزندی را پیدا می کنیم که بتواند شامل عدد مورد نظر شود .
3 . اگر فرزند فرزندی نداشت عدد را به همان گره اضافه می کنیم .
• در غیر اینصورت به سراغ فرزند می رویم و همین کار را تکرار می کنیم .
برای حذف کردن یک عنصر از درخت 2 - 3 - 4 1 . عنصر مورد نظر را پیدا می کنیم



wiki: درخت ۲–۳ ۴
