در علم رایانه، ساختمان داده درخت ۲ - ۳، یک نوع درخت جستجوی خودمتوازن است. درخت های جستجوی دودویی ممکن است با درج ها و حذف های گوناگون، حالت توازن خود را از دست بدهند. حالتی را در نظر بگیرید که یک درخت دودویی جستجو دارید و n داده را که اتفاقاً از کوچک به بزرگ مرتب هستند به ترتیب در آن درج می کنید. در این حالت، این درخت عملاً به یک لیست پیوندی تبدیل می شود که جستجو در آن از مرتبه ( O ( n است و گذشته از این که مزیت استفاده از د. د. ج ( درخت دودویی جستجو ) از بین رفته، مقدار زیادی حافظه هم با اختصاص دادن به اشاره گرهای تهی از دست می رود. پیاده سازی توابع درج و حذف درخت ۲ - ۳ به گونه ای است که این درخت طی درج ها و حذف ها به صورت متوازن باقی می ماند.
درخت ۲ - ۳ سه نوع گره دارد:
• گره برگ که فقط یک مقدار دارد.
• گرهِ ۲
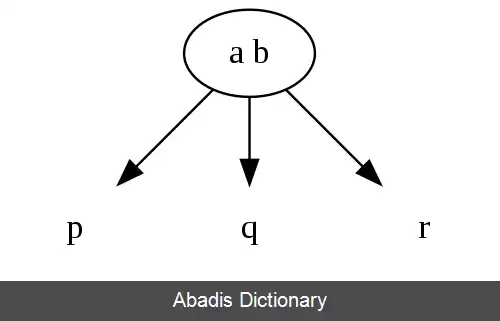
• گرهِ ۳
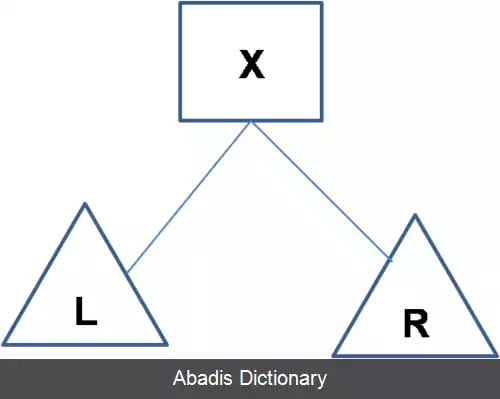
در گره ۲، X مقدار گره، L زیردرخت سمت چپ و R زیردرخت راست گره است. هر گره ۲ باید خصوصیات زیر را داشته باشد:
• هر مقدار در L {\displaystyle L} باید کوچک تر از X {\displaystyle X} باشد.
• هر مقدار در R {\displaystyle R} باید بزرگ تر از X {\displaystyle X} باشد.
• طول مسیرها از ریشه به برگ های هریک از زیردرخت ها باید یکسان باشد.
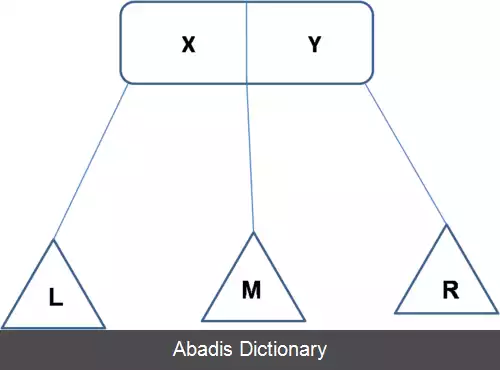
در گره ۳، X مقدار گره، L زیردرخت سمت چپ، M زیردرخت میانی و R زیردرخت راست گره است. هر گره ۳ باید خصوصیات زیر را داشته باشد:
• هر مقدار در L {\displaystyle L} باید کوچک تر از X {\displaystyle X} باشد.
• هر مقدار در R {\displaystyle R} باید بزرگ تر از X {\displaystyle X} و کوچک تر از Y {\displaystyle Y} باشد.
• هر مقدار در R {\displaystyle R} باید بزرگ تر از Y {\displaystyle Y} باشد.
• طول مسیرها از ریشه به برگ های هریک از زیردرخت ها باید یکسان باشد.
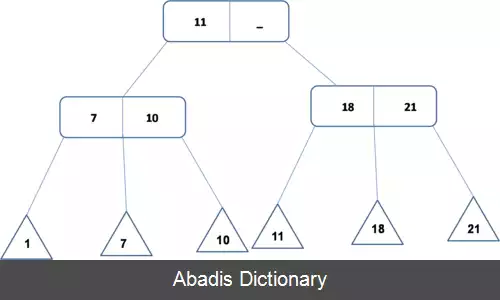
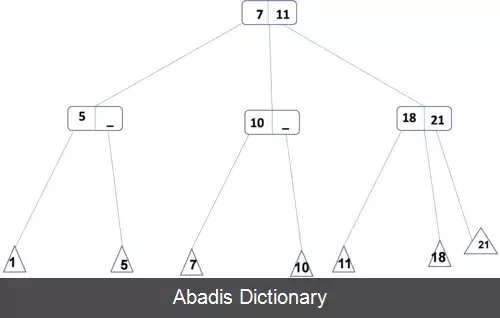
باید توجه داشت که همه مقادیر در گره های برگ وجود دارند و گره های داخلی فقط برای هدایت جستجو ایجاد شده اند. هر گره داخلی یک گره ۳ ( با دو یا سه فرزند ) است که مقدار X آن برابر با کوچک ترین مقدار موجود در زیردرخت دوم و مقدار Y آن ( در صورت وجود ) برابر با کوچک ترین مقدار موجود در زیردرخت سوم است.
همان طور که گفته شد اطلاعات ذخیره شده در گره های داخلی باعث آسان شدن جستجو می شود. فرض کنید می خواهیم عنصر n را جستجو کنیم. از ریشه شروع می کنیم و به ترتیب زیر به سمت برگ ها می رویم: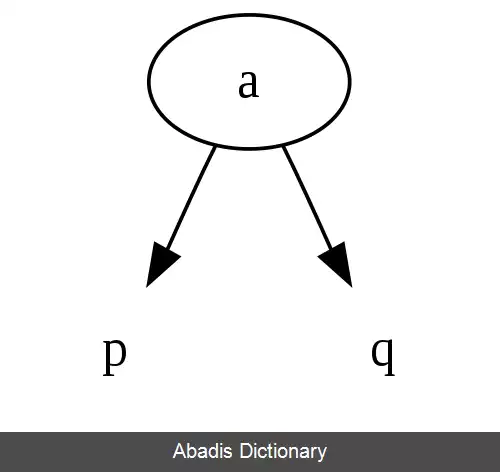
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدرخت ۲ - ۳ سه نوع گره دارد:
• گره برگ که فقط یک مقدار دارد.
• گرهِ ۲
• گرهِ ۳
در گره ۲، X مقدار گره، L زیردرخت سمت چپ و R زیردرخت راست گره است. هر گره ۲ باید خصوصیات زیر را داشته باشد:
• هر مقدار در L {\displaystyle L} باید کوچک تر از X {\displaystyle X} باشد.
• هر مقدار در R {\displaystyle R} باید بزرگ تر از X {\displaystyle X} باشد.
• طول مسیرها از ریشه به برگ های هریک از زیردرخت ها باید یکسان باشد.
در گره ۳، X مقدار گره، L زیردرخت سمت چپ، M زیردرخت میانی و R زیردرخت راست گره است. هر گره ۳ باید خصوصیات زیر را داشته باشد:
• هر مقدار در L {\displaystyle L} باید کوچک تر از X {\displaystyle X} باشد.
• هر مقدار در R {\displaystyle R} باید بزرگ تر از X {\displaystyle X} و کوچک تر از Y {\displaystyle Y} باشد.
• هر مقدار در R {\displaystyle R} باید بزرگ تر از Y {\displaystyle Y} باشد.
• طول مسیرها از ریشه به برگ های هریک از زیردرخت ها باید یکسان باشد.
باید توجه داشت که همه مقادیر در گره های برگ وجود دارند و گره های داخلی فقط برای هدایت جستجو ایجاد شده اند. هر گره داخلی یک گره ۳ ( با دو یا سه فرزند ) است که مقدار X آن برابر با کوچک ترین مقدار موجود در زیردرخت دوم و مقدار Y آن ( در صورت وجود ) برابر با کوچک ترین مقدار موجود در زیردرخت سوم است.
همان طور که گفته شد اطلاعات ذخیره شده در گره های داخلی باعث آسان شدن جستجو می شود. فرض کنید می خواهیم عنصر n را جستجو کنیم. از ریشه شروع می کنیم و به ترتیب زیر به سمت برگ ها می رویم:






wiki: درخت ۲–۳
