درخت گسترده ( به انگلیسی: Splay tree ) یک درخت جستجوی دودویی خود متوازن است؛ که قابلیت اصلی آن تسهیل فرایند دسترسی به اطلاعاتی است که جدیداً به آن ها مراجعه کرده ایم. این درخت اعمال اصلی مانند درج و جستجو و حذف را در O ( l g n ) انجام می دهد. برای بسیاری از دنباله های غیر تصادفی، این درخت بهتر از سایر درخت های جستجو عمل می کند. درخت اسپلی توسط دانیل اسلیتور و رابرت تارجان در سال ۱۹۸۵ ابداع شد.
در این درخت همهٔ عملیات معمول در درخت جستجوی دودویی با عمل پایه گسترش ترکیب می شوند. به این معنی که برای یک عنصر خاص درخت را باز می آراید تا عنصر در ریشهٔ درخت قرار بگیرد. یک راه انجام این کار این است که ابتدا یک جستجو برای یافتن عنصر مورد نظر انجام دهیم و سپس آن را به بالای درخت برسانیم.
• کارایی بهتر: کارایی بهتر برای یک درخت گسترده به خود متوازنی آن بستگی دارد و به این که عناصری که بارها دسترسی یافته اند به ریشه نزدیکتر شوند تا سریعتر مورد دسترسی قرار بگیرند. این تقریباً برای تمام کاربردهای عملی این ساختار مزیتی است که برای پیاده سازی حافظه نهان و الگوریتم بازیافت حافظه بسیار مفید است. این ساختار هنگامی کارآمدتر خواهد بود که دسترسی به صورت یک پارچه نباشد.
• پیاده سازی ساده تر: پیاده سازی ساده تری نسبت به دیگر درخت های جستجوی دودویی خود متوازن، مانند درخت قرمز سیاه یا درخت ای وی ال دارد.
• امکان ایجاد یک نسخه پایدار: که اجازه دسترسی به هر دو نسخه قبلی و جدید را پس از بروزرسانی می دهد. این می تواند در برنامه نویسی تابعی مفید باشد و به O ( l g n ) {\displaystyle O ( lgn ) } فضا در هر بروزرسانی نیاز دارد.
• بر خلاف سایر انواع درختان خود متوازن به خوبی با گره حاوی کلیدهای هویت کار می کند. حتی با وجود کلیدهای هویت، عملکرد در O ( l g n ) {\displaystyle O ( lgn ) } باقی می ماند. یک طراحی دقیق عملیات پیدا کردن می تواند چپ ترین یا راست ترین گرهٔ کلید داده شده را برگرداند.
• درختانی می توانند وجود داشته باشند که توزیع دادهٔ ورودی را کمی سریع تر انجام می دهند.
• عملکرد ضعیف در دسترسی یکنواخت: عملکرد درخت گسترده به طور قابل توجهی بدتر از درخت جستجوی دودویی متعادل ساده برای دسترسی یکنواخت است.
• یکی از بدترین حالت های الگوریتم درخت گسترده دسترسی ترتیبی به همه عناصر در درخت مرتب شده است که درخت را کاملاً نامتعادل می کند ( این n دسترسی دارد که هرکدام از O ( l g n ) {\displaystyle O ( lgn ) } است ) . دوباره مورد دسترسی قرار دادن عنصر اول، باعث می شود که عملیاتی که از O ( n ) {\displaystyle O ( n ) } است اجرا شود تا درخت دوباره متوازن شود ( قبل بازگشت عنصر اول ) . این تأخیر قابل توجهی برای عملیات نهایی است، با این حال، تحقیقات اخیر نشان می دهد که متعادل سازی تصادفی می تواند از اثر عدم تعادل جلوگیری کند و بازدهی مشابه سایر الگوریتم های خود متوازن بدهد.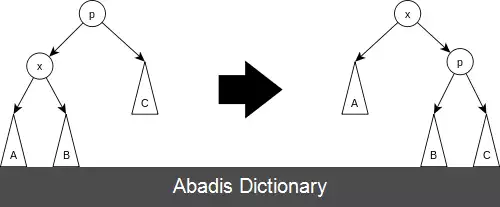
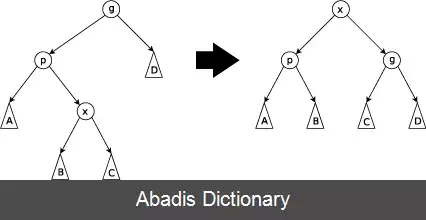
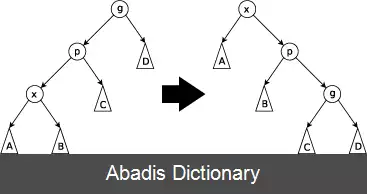
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر این درخت همهٔ عملیات معمول در درخت جستجوی دودویی با عمل پایه گسترش ترکیب می شوند. به این معنی که برای یک عنصر خاص درخت را باز می آراید تا عنصر در ریشهٔ درخت قرار بگیرد. یک راه انجام این کار این است که ابتدا یک جستجو برای یافتن عنصر مورد نظر انجام دهیم و سپس آن را به بالای درخت برسانیم.
• کارایی بهتر: کارایی بهتر برای یک درخت گسترده به خود متوازنی آن بستگی دارد و به این که عناصری که بارها دسترسی یافته اند به ریشه نزدیکتر شوند تا سریعتر مورد دسترسی قرار بگیرند. این تقریباً برای تمام کاربردهای عملی این ساختار مزیتی است که برای پیاده سازی حافظه نهان و الگوریتم بازیافت حافظه بسیار مفید است. این ساختار هنگامی کارآمدتر خواهد بود که دسترسی به صورت یک پارچه نباشد.
• پیاده سازی ساده تر: پیاده سازی ساده تری نسبت به دیگر درخت های جستجوی دودویی خود متوازن، مانند درخت قرمز سیاه یا درخت ای وی ال دارد.
• امکان ایجاد یک نسخه پایدار: که اجازه دسترسی به هر دو نسخه قبلی و جدید را پس از بروزرسانی می دهد. این می تواند در برنامه نویسی تابعی مفید باشد و به O ( l g n ) {\displaystyle O ( lgn ) } فضا در هر بروزرسانی نیاز دارد.
• بر خلاف سایر انواع درختان خود متوازن به خوبی با گره حاوی کلیدهای هویت کار می کند. حتی با وجود کلیدهای هویت، عملکرد در O ( l g n ) {\displaystyle O ( lgn ) } باقی می ماند. یک طراحی دقیق عملیات پیدا کردن می تواند چپ ترین یا راست ترین گرهٔ کلید داده شده را برگرداند.
• درختانی می توانند وجود داشته باشند که توزیع دادهٔ ورودی را کمی سریع تر انجام می دهند.
• عملکرد ضعیف در دسترسی یکنواخت: عملکرد درخت گسترده به طور قابل توجهی بدتر از درخت جستجوی دودویی متعادل ساده برای دسترسی یکنواخت است.
• یکی از بدترین حالت های الگوریتم درخت گسترده دسترسی ترتیبی به همه عناصر در درخت مرتب شده است که درخت را کاملاً نامتعادل می کند ( این n دسترسی دارد که هرکدام از O ( l g n ) {\displaystyle O ( lgn ) } است ) . دوباره مورد دسترسی قرار دادن عنصر اول، باعث می شود که عملیاتی که از O ( n ) {\displaystyle O ( n ) } است اجرا شود تا درخت دوباره متوازن شود ( قبل بازگشت عنصر اول ) . این تأخیر قابل توجهی برای عملیات نهایی است، با این حال، تحقیقات اخیر نشان می دهد که متعادل سازی تصادفی می تواند از اثر عدم تعادل جلوگیری کند و بازدهی مشابه سایر الگوریتم های خود متوازن بدهد.



wiki: درخت گسترده
