درخت پوشای کمینه یا درخت فراگیر مینیمم در گراف های ارزش دار ( وزن دار ) ساخته می شود.
فرض کنید گراف یک گراف همبند باشد ( یعنی بین هردو رأس متمایز آن یک مسیر وجود داشته باشد ) منظور از یک درخت پوشا از این گراف درختی است که شامل همه رئوس این گراف باشد ولی فقط بعضی از یال های آن را دربر گیرد. منظور از درخت پوشای مینیمم ( برای گراف همبند وزن دار ) درختی است که بین درخت های پوشای آن گراف، مجموع وزن یال های آن، کمترین مقدار ممکن باشد. برای به دست آوردن درخت پوشای بهینه یک گراف جهت دار متصل می توان از الگوریتم های متفاوتی استفاده نمود. پنج الگوریتم معروف پیدا کردن درخت پوشای کمینه عبارتند از: الگوریتم کروسکال، الگوریتم پریم، الگوریتم بروکا ( سولین ) ، الگوریتم حذف معکوس و الگوریتم فلوید - وارشال
تعداد حالات ممکن:
امکان وجود بیش از یک درخت پوشای کمینه وجود دارد، برای مثال اگر تمام یال ها وزن برابری داشته باشند، تمام زیر در خت ها درخت پوشای کمینه هستند. اگر وزن هر دو یال با هم متفاوت باشد، تنها یک درخت پوشای کمینه خواهیم داشت.
کم وزن ترین یال در برش گراف:
ادعا: اگر گراف را به دو مجموعه V و V′ از راس ها افراز کنیم، کم وزن ترین یال بین یال هایی که یک طرفشان در مجموعه V و طرف دیگرشان در مجموعه V′ است باید جزء درخت پوشای کمینه باشد. ( اگر چند یال با کم ترین وزن وجود داشت، باید دقیقاً یکی از آن ها جزء درخت پوشای کمینه باشد ) .
کم وزن ترین یال گراف:
اگر کم وزن ترین یال گراف یکتا باشد در هر درخت پوشای کمینه ای وجود خواهد داشت.
پروزن ترین یال هر دور:
اگر یالی در یک دور از تمام یال های موجود در آن دور وزنش بیشتر باشد، نمی تواند در درخت پوشای کمینه قرار بگیرد. فرض خلف: فرض کنید این یال در یک درخت پوشای کمینه وجود دارد، اگر آن را حذف کنیم درخت به دو مؤلف تقسیم می شود و دور مذکور در گراف اصلی بدون این یال یک مسیر بین این دو مؤلفه می شود. یالی از این مسیر که این مسیر را از این مؤلفه به آن مؤلفه منتقل می کند جایگزین یال حذف شده به درخت اضافه کنید ( ممکن است چند یال این کار را بکنند که مهم نیست کدام را انتخاب می کنیم ) . این یال کم وزن تر است پس مجموع وزن های یال های درخت جدید کم تر است که با کمینه بودن درخت اول در تناقض است.
در مسائلی که هدف ایجاد شبکه ای است که برای ایجاد ارتباط بین هر دو عضو آن هزینه ای باید بپردازیم و می خواهیم در نهایت در این شبکه بین هر دو عضو ارتباط وجود داشته باشد، درخت پوشای کمینه همان کم هزینه ترین شبکه است. برای مثال فرض کنید در کشوری می خواهیم طوری جاده سازی کنیم که بتوان از هر شهری به هر شهر دیگری سفر کرد و هزینه ساخت جاده بین هر دو شهر را داریم ( این هزینه می تواند تابعی بر اساس فاصله ۲ شهر، آب و هوای بین دو شهر فاصله آن ها از شرکت راه سازی و … باشد ) . برای پیدا کردن کم هزینه ترین راه، باید درخت پوشای کمینه را بیابیم.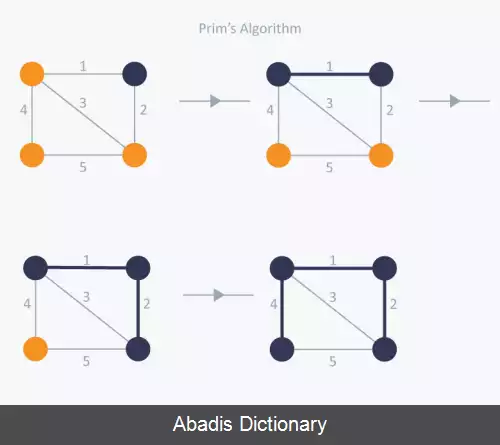
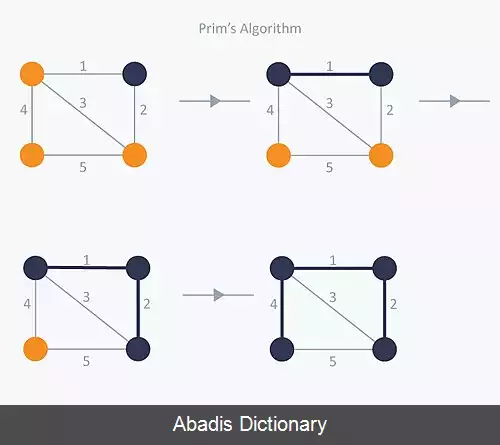

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنید گراف یک گراف همبند باشد ( یعنی بین هردو رأس متمایز آن یک مسیر وجود داشته باشد ) منظور از یک درخت پوشا از این گراف درختی است که شامل همه رئوس این گراف باشد ولی فقط بعضی از یال های آن را دربر گیرد. منظور از درخت پوشای مینیمم ( برای گراف همبند وزن دار ) درختی است که بین درخت های پوشای آن گراف، مجموع وزن یال های آن، کمترین مقدار ممکن باشد. برای به دست آوردن درخت پوشای بهینه یک گراف جهت دار متصل می توان از الگوریتم های متفاوتی استفاده نمود. پنج الگوریتم معروف پیدا کردن درخت پوشای کمینه عبارتند از: الگوریتم کروسکال، الگوریتم پریم، الگوریتم بروکا ( سولین ) ، الگوریتم حذف معکوس و الگوریتم فلوید - وارشال
تعداد حالات ممکن:
امکان وجود بیش از یک درخت پوشای کمینه وجود دارد، برای مثال اگر تمام یال ها وزن برابری داشته باشند، تمام زیر در خت ها درخت پوشای کمینه هستند. اگر وزن هر دو یال با هم متفاوت باشد، تنها یک درخت پوشای کمینه خواهیم داشت.
کم وزن ترین یال در برش گراف:
ادعا: اگر گراف را به دو مجموعه V و V′ از راس ها افراز کنیم، کم وزن ترین یال بین یال هایی که یک طرفشان در مجموعه V و طرف دیگرشان در مجموعه V′ است باید جزء درخت پوشای کمینه باشد. ( اگر چند یال با کم ترین وزن وجود داشت، باید دقیقاً یکی از آن ها جزء درخت پوشای کمینه باشد ) .
کم وزن ترین یال گراف:
اگر کم وزن ترین یال گراف یکتا باشد در هر درخت پوشای کمینه ای وجود خواهد داشت.
پروزن ترین یال هر دور:
اگر یالی در یک دور از تمام یال های موجود در آن دور وزنش بیشتر باشد، نمی تواند در درخت پوشای کمینه قرار بگیرد. فرض خلف: فرض کنید این یال در یک درخت پوشای کمینه وجود دارد، اگر آن را حذف کنیم درخت به دو مؤلف تقسیم می شود و دور مذکور در گراف اصلی بدون این یال یک مسیر بین این دو مؤلفه می شود. یالی از این مسیر که این مسیر را از این مؤلفه به آن مؤلفه منتقل می کند جایگزین یال حذف شده به درخت اضافه کنید ( ممکن است چند یال این کار را بکنند که مهم نیست کدام را انتخاب می کنیم ) . این یال کم وزن تر است پس مجموع وزن های یال های درخت جدید کم تر است که با کمینه بودن درخت اول در تناقض است.
در مسائلی که هدف ایجاد شبکه ای است که برای ایجاد ارتباط بین هر دو عضو آن هزینه ای باید بپردازیم و می خواهیم در نهایت در این شبکه بین هر دو عضو ارتباط وجود داشته باشد، درخت پوشای کمینه همان کم هزینه ترین شبکه است. برای مثال فرض کنید در کشوری می خواهیم طوری جاده سازی کنیم که بتوان از هر شهری به هر شهر دیگری سفر کرد و هزینه ساخت جاده بین هر دو شهر را داریم ( این هزینه می تواند تابعی بر اساس فاصله ۲ شهر، آب و هوای بین دو شهر فاصله آن ها از شرکت راه سازی و … باشد ) . برای پیدا کردن کم هزینه ترین راه، باید درخت پوشای کمینه را بیابیم.



wiki: درخت پوشای کمینه
