در علوم رایانه، یک درخت پسوندی ( درخت PAT، که با نام قدیمی تر درخت موقعیت نیز شناخته شده است ) یک ترای شامل پسوندهای یک رشته ی داده شده به عنوان کلید و مکان آنها در رشته به عنوان مقدار است. درخت های پسوندی پیاده سازی سریع شمار زیادی از عملیات های رشته ای مهم را ممکن می سازند.
درخت پسوندی برای یک رشتهٔ S ، درختی است که یال های آن با رشته هایی برچسب خورده اند، به طوری که هر پسوند S ، متناظر با دقیقاً یک مسیر از ریشهٔ درخت به یک برگ است؛ بنابراین، این درخت، یک درخت مبنا برای پسوندهای S خواهد بود.
ساخت چنین درختی برای رشتهٔ S به زمان و فضای خطی بر حسب طول S نیاز دارد. وقتی این درخت ساخته شود، عملیات رشته ای، مانند یافتن یک زیررشته در S ، یافتن یک زیررشته با یک تعداد مجاز مشخص شده برای خطاها، یافتن تطابق ها برای یک الگوی عبارت باقاعده و غیره، می توانند به سرعت انجام شوند. درخت های پسوندی یکی از اولین راه حل های با زمان خطی برای مسئلهٔ بزرگترین زیررشته مشترک را نیز میسر ساخته اند. این افزایش سرعت ها هزینه ای دارند: ذخیره سازی یک درخت پسوندی برای یک رشته، معمولاً به فضای بیشتری نسبت به ذخیره سازی خود رشته نیاز دارد.
درخت پسوندی برای رشتهٔ S با طول n درختی است که در شرایط زیر صدق کند:
• دقیقا دارای n برگ است که از 1 تا n شماره گذاری شده اند.
• تمامی گره های داخلی ( در بعضی موارد، به جز ریشه ) حداقل دو فرزند دارند.
• هر یال با یک زیررشته ی ناتهی از S {\displaystyle S} برچسب خورده است.
• هیچ دو یالی که از یک گره بیرون می آیند نمی توانند برچسب هایی داشته باشند که با یک کاراکتر شروع می شوند.
• رشته ی بدست آمده از الحاق زیررشته های مسیر از ریشه تا برگ iاُم، معرف پسوند S {\displaystyle S} برای هر i از 1 تا n است.
از آنجایی که یک اینچنین درختی برای همهٔ رشته ها وجود ندارد، به انتهای S ، یک کاراکتر ترمینال ( معمولاً با $ نشان می دهند ) که در الفبای اصلی وجود ندارد الحاق می شود. مثلا اگر سعی کنید برای رشته abab آن را بسازید متوجه این نکته می شوید چون پسوند ab پیشوند پسوند رشته کامل ( abab ) است. از آنجایی که تمامی گره های داخلی به جز ریشه شاخه شاخه می شوند، تعداد این گره ها حداکثر n − 1 خواهد بود و تعداد کل گره ها برابر خواهد بود با n + ( n − 1 ) + 1 = 2 n ( n برگ، n − 1 گره داخلی، و یک ریشه ) .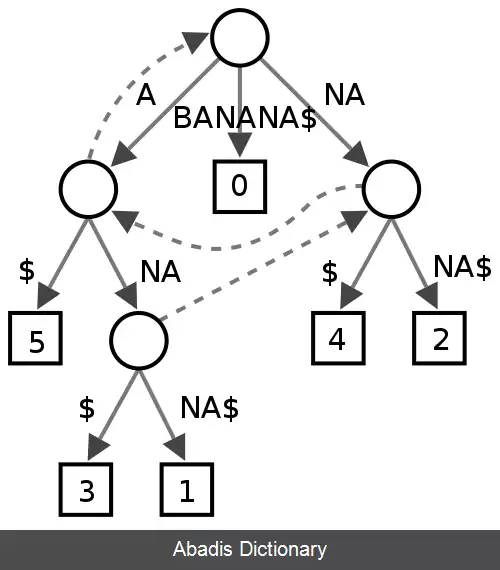
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدرخت پسوندی برای یک رشتهٔ S ، درختی است که یال های آن با رشته هایی برچسب خورده اند، به طوری که هر پسوند S ، متناظر با دقیقاً یک مسیر از ریشهٔ درخت به یک برگ است؛ بنابراین، این درخت، یک درخت مبنا برای پسوندهای S خواهد بود.
ساخت چنین درختی برای رشتهٔ S به زمان و فضای خطی بر حسب طول S نیاز دارد. وقتی این درخت ساخته شود، عملیات رشته ای، مانند یافتن یک زیررشته در S ، یافتن یک زیررشته با یک تعداد مجاز مشخص شده برای خطاها، یافتن تطابق ها برای یک الگوی عبارت باقاعده و غیره، می توانند به سرعت انجام شوند. درخت های پسوندی یکی از اولین راه حل های با زمان خطی برای مسئلهٔ بزرگترین زیررشته مشترک را نیز میسر ساخته اند. این افزایش سرعت ها هزینه ای دارند: ذخیره سازی یک درخت پسوندی برای یک رشته، معمولاً به فضای بیشتری نسبت به ذخیره سازی خود رشته نیاز دارد.
درخت پسوندی برای رشتهٔ S با طول n درختی است که در شرایط زیر صدق کند:
• دقیقا دارای n برگ است که از 1 تا n شماره گذاری شده اند.
• تمامی گره های داخلی ( در بعضی موارد، به جز ریشه ) حداقل دو فرزند دارند.
• هر یال با یک زیررشته ی ناتهی از S {\displaystyle S} برچسب خورده است.
• هیچ دو یالی که از یک گره بیرون می آیند نمی توانند برچسب هایی داشته باشند که با یک کاراکتر شروع می شوند.
• رشته ی بدست آمده از الحاق زیررشته های مسیر از ریشه تا برگ iاُم، معرف پسوند S {\displaystyle S} برای هر i از 1 تا n است.
از آنجایی که یک اینچنین درختی برای همهٔ رشته ها وجود ندارد، به انتهای S ، یک کاراکتر ترمینال ( معمولاً با $ نشان می دهند ) که در الفبای اصلی وجود ندارد الحاق می شود. مثلا اگر سعی کنید برای رشته abab آن را بسازید متوجه این نکته می شوید چون پسوند ab پیشوند پسوند رشته کامل ( abab ) است. از آنجایی که تمامی گره های داخلی به جز ریشه شاخه شاخه می شوند، تعداد این گره ها حداکثر n − 1 خواهد بود و تعداد کل گره ها برابر خواهد بود با n + ( n − 1 ) + 1 = 2 n ( n برگ، n − 1 گره داخلی، و یک ریشه ) .

wiki: درخت پسوندی
