درخت مسابقه ( به انگلیسی: Tournament tree ) یک نوع درخت دودویی است. درخت مسابقه به دو نوع درخت برنده و درخت بازنده تقسیم می شود. راس های درخت مسابقه به دو نوع رئوس خارجی ( برگ ها ) و رئوس داخلی ( رئوس غیر برگ ) تقسیم بندی می شوند. راس های خارجی نماینده بازیکنان هستند و رئوس داخلی هر کدام نتیجه تک مسابقه ( به انگلیسی: Match ) بین برنده های دو زیر درخت خود را در خود نگه می دارند.
در درخت برنده ( به انگلیسی: Winner tree ) هر راس داخلی باید بازیکن برنده بین دو راس فرزند خود را ذخیره کند و در انتها ریشه درخت حاوی بازیکنی خواهد بود که در تمام تک مسابقه ها برنده شده است. اگر برنده را در هر تک مسابقه بازیکنی در نظر بگیریم که مقدار آن کمتر است، در این صورت ریشه درخت اشاره به بازیکنی خواهد داشت که کمترین مقدار را بین تمام بازیکنان دارد. از کاربردهای این داده ساختار می توان به الگوریتم مرتب سازی مسابقه ای اشاره نمود.
• ایجاد درخت: O ( n ) {\displaystyle O ( n ) }
رئوس خارجی نماینده عناصر می شوند و سپس هر راس داخلی برنده بین دو فرزند خود را ذخیره کرده و به این ترتیب تا ریشه پیش می رویم. در نهایت ریشه حاوی برندهٔ نهایی ( عنصر کمینه یا بیشینه ) بین تمام عناصر خواهد بود. به دلیل اینکه تعداد کل رئوس ضریبی از تعداد عناصر می شود، در نتیجه زمان ایجاد درخت از O ( n ) است.
• حذف عنصر کمینه ( بیشینه ) : O ( log n ) {\displaystyle O ( \log n ) }
زمانی که بخواهیم عنصر کمینه ( بیشینه ) را حذف کنیم، مقدار آن را مثبت بی نهایت ( منفی بی نهایت ) می کنیم و سپس تک مسابقاتی که روی مسیر بین آن عنصر و ریشه وجود دارد را دوباره انجام می دهیم تا درخت جدید ساخته شود. چون ارتفاع درخت از O ( log n ) است زمان حذف از O ( log n ) می شود.
• جایگزینی عنصر کمینه ( بیشینه ) : O ( log n ) {\displaystyle O ( \log n ) }
زمانی که بخواهیم عنصر کمینه ( بیشینه ) را جایگزین کنیم، مقدار جدید را به آن می دهیم و سپس تک مسابقاتی که روی مسیر بین آن عنصر و ریشه وجود دارد را دوباره انجام می دهیم تا درخت جدید ساخته شود. چون ارتفاع درخت از O ( log n ) است زمان جایگزینی نیز از O ( log n ) می شود.
در ادامه پیاده سازی درخت برنده با استفاده از آرایه به زبان پایتون آمده است.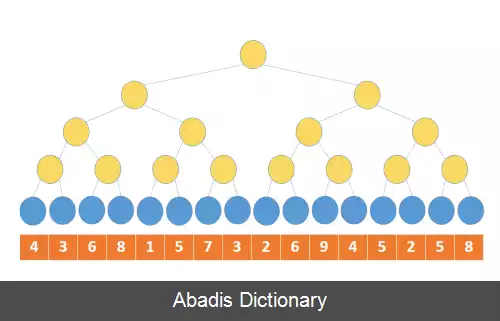
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر درخت برنده ( به انگلیسی: Winner tree ) هر راس داخلی باید بازیکن برنده بین دو راس فرزند خود را ذخیره کند و در انتها ریشه درخت حاوی بازیکنی خواهد بود که در تمام تک مسابقه ها برنده شده است. اگر برنده را در هر تک مسابقه بازیکنی در نظر بگیریم که مقدار آن کمتر است، در این صورت ریشه درخت اشاره به بازیکنی خواهد داشت که کمترین مقدار را بین تمام بازیکنان دارد. از کاربردهای این داده ساختار می توان به الگوریتم مرتب سازی مسابقه ای اشاره نمود.
• ایجاد درخت: O ( n ) {\displaystyle O ( n ) }
رئوس خارجی نماینده عناصر می شوند و سپس هر راس داخلی برنده بین دو فرزند خود را ذخیره کرده و به این ترتیب تا ریشه پیش می رویم. در نهایت ریشه حاوی برندهٔ نهایی ( عنصر کمینه یا بیشینه ) بین تمام عناصر خواهد بود. به دلیل اینکه تعداد کل رئوس ضریبی از تعداد عناصر می شود، در نتیجه زمان ایجاد درخت از O ( n ) است.
• حذف عنصر کمینه ( بیشینه ) : O ( log n ) {\displaystyle O ( \log n ) }
زمانی که بخواهیم عنصر کمینه ( بیشینه ) را حذف کنیم، مقدار آن را مثبت بی نهایت ( منفی بی نهایت ) می کنیم و سپس تک مسابقاتی که روی مسیر بین آن عنصر و ریشه وجود دارد را دوباره انجام می دهیم تا درخت جدید ساخته شود. چون ارتفاع درخت از O ( log n ) است زمان حذف از O ( log n ) می شود.
• جایگزینی عنصر کمینه ( بیشینه ) : O ( log n ) {\displaystyle O ( \log n ) }
زمانی که بخواهیم عنصر کمینه ( بیشینه ) را جایگزین کنیم، مقدار جدید را به آن می دهیم و سپس تک مسابقاتی که روی مسیر بین آن عنصر و ریشه وجود دارد را دوباره انجام می دهیم تا درخت جدید ساخته شود. چون ارتفاع درخت از O ( log n ) است زمان جایگزینی نیز از O ( log n ) می شود.
در ادامه پیاده سازی درخت برنده با استفاده از آرایه به زبان پایتون آمده است.

wiki: درخت مسابقه
