درعلوم کامپیوتر، درخت محدوده یک ساختمان داده از نوع درخت مرتب است که لیستی از نقاط را نگه می دارد. این درخت تمامی نقاط داخل یک بازه را به صورت بهینه گزارش می دهد و معمولاً در دو بعد یا بیشتر استفاده می شود. درختهای محدوده توسط جان لوئیس بنتلی در سال ۱۹۷۹ معرفی شدند. [ ۱] ساختمان داده های مشابه نیز به صورت مستقل توسط لوکر[ ۲] ، لی و وانگ[ ۳] و ویللرد[ ۴] معرفی شدند. درخت محدوده یک جایگزین برای درخت کی دی است. در مقایسه با درختهای کی دی، درختهای محدوده زمان جستجو سریعتری از مرتبه ( O ( logd n + k دارند ولی حافظه بیشتری از مرتبه ( O ( n logd−۱ n استفاده می کنند که n تعداد نقاط ذخیره شده در درخت، d بعد هر نقطه و k تعداد نقاط به دست آمده از جستجوی مورد نظر است.
درخت محدوده روی مجموعهای از نقاط یک بعدی، یک درخت جستجوی دودویی متوازن روی آن نقاط است. نقاط در برگ های درخت ذخیره می شوند. هر گرهٔ داخلی، بیشترین مقدار ذخیره شده در زیر درخت چپ خود را نگه می دارد. یک درخت محدوده روی مجموعه ای از نقاط d بعدی، یک درخت جستجوی دودویی بازگشتی در چندین سطح است. هر سطح از این ساختمان داده یک درخت جستجوی دودویی روی یکی از d بعد است. اولین سطح درخت محدوده یک درخت جستجوی دودویی روی اولین مؤلفه است. هر رأس v از این درخت، یک درخت محدوده ( d - 1 ) بعدی روی ( d - 1 ) مؤلفه آخر نقاط ذخیره شده در زیر درخت v است.
درخت محدوده یک بعدی روی مجموعه ای از n نقطه، یک درخت جستجو دودویی است که می تواند در زمان ( O ( n log n ساخته شود. درختهای محدوده در ابعاد بالاتر را به صورت بازگشتی این گونه می سازیم: ابتدا یک درخت جستجوی دودویی متوازن روی مؤلفه اول نقاط می سازیم. سپس، برای هر رأس v در این درخت، یک درخت محدوده ( d - 1 ) بعدی روی نقاط زیر درخت v می سازیم. ساختن درخت محدوده با این روش به زمان ( O ( n logdn نیاز دارد.
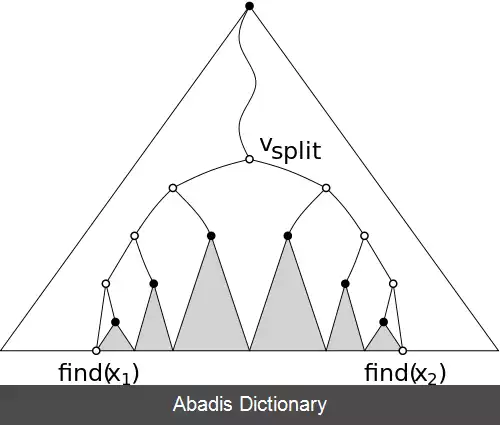
با توجه به اینکه یک درخت محدوده روی مجموعهای از نقاط دو بعدی می تواند در زمان ( O ( n log n ساخته شود، می توانیم روش فوق را ارتقا دهیم. [ ۵] فرض کنید S مجموعه ای n تایی از نقاط دو بعدی است. اگر S فقط یک نقطه داشته باشد، برگ شامل آن نقطه را بر گردانید. در غیر این صورت، ساختار مرتبط با S؛ یک درخت محدوده یک بعدی روی مختصات y نقاط S را بسازید. xm را میانهٔ مؤلفه های x نقاط در نظر بگیرید. SL مجموعه نقاطی است که مختصات x شان کمتر یا مساوی xm و SR مجموعه نقاطی است که مختصات x شان بیشتر از xm است. به صورت بازگشتی vL، یک درخت محدوده دو بعدی روی SL و vR، یک درخت محدوده دو بعدی روی SR، را بسازید. رأس v را با فرزند چپ vL و فرزند راست vR بسازید. اگر در ابتدای الگوریتم این نقاط را برحسب مختصات y شان مرتب کنیم و این ترتیب هنگام جدا کردن نقاط برحسب x شان تغییر نکند، می توانیم ساختارهای مرتبط با هریک از درخت ها را در زمان خطی بسازیم. این راه، زمان ساخته شدن درخت محدودهٔ دوبعدی را به ( O ( n logn کاهش می دهد، که همچنین زمان ساخت درخت محدوده d بعدی نیز به مرتبهٔ ( O ( n logd−۱n کاهش می یابد.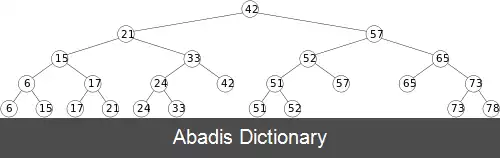
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدرخت محدوده روی مجموعهای از نقاط یک بعدی، یک درخت جستجوی دودویی متوازن روی آن نقاط است. نقاط در برگ های درخت ذخیره می شوند. هر گرهٔ داخلی، بیشترین مقدار ذخیره شده در زیر درخت چپ خود را نگه می دارد. یک درخت محدوده روی مجموعه ای از نقاط d بعدی، یک درخت جستجوی دودویی بازگشتی در چندین سطح است. هر سطح از این ساختمان داده یک درخت جستجوی دودویی روی یکی از d بعد است. اولین سطح درخت محدوده یک درخت جستجوی دودویی روی اولین مؤلفه است. هر رأس v از این درخت، یک درخت محدوده ( d - 1 ) بعدی روی ( d - 1 ) مؤلفه آخر نقاط ذخیره شده در زیر درخت v است.
درخت محدوده یک بعدی روی مجموعه ای از n نقطه، یک درخت جستجو دودویی است که می تواند در زمان ( O ( n log n ساخته شود. درختهای محدوده در ابعاد بالاتر را به صورت بازگشتی این گونه می سازیم: ابتدا یک درخت جستجوی دودویی متوازن روی مؤلفه اول نقاط می سازیم. سپس، برای هر رأس v در این درخت، یک درخت محدوده ( d - 1 ) بعدی روی نقاط زیر درخت v می سازیم. ساختن درخت محدوده با این روش به زمان ( O ( n logdn نیاز دارد.
با توجه به اینکه یک درخت محدوده روی مجموعهای از نقاط دو بعدی می تواند در زمان ( O ( n log n ساخته شود، می توانیم روش فوق را ارتقا دهیم. [ ۵] فرض کنید S مجموعه ای n تایی از نقاط دو بعدی است. اگر S فقط یک نقطه داشته باشد، برگ شامل آن نقطه را بر گردانید. در غیر این صورت، ساختار مرتبط با S؛ یک درخت محدوده یک بعدی روی مختصات y نقاط S را بسازید. xm را میانهٔ مؤلفه های x نقاط در نظر بگیرید. SL مجموعه نقاطی است که مختصات x شان کمتر یا مساوی xm و SR مجموعه نقاطی است که مختصات x شان بیشتر از xm است. به صورت بازگشتی vL، یک درخت محدوده دو بعدی روی SL و vR، یک درخت محدوده دو بعدی روی SR، را بسازید. رأس v را با فرزند چپ vL و فرزند راست vR بسازید. اگر در ابتدای الگوریتم این نقاط را برحسب مختصات y شان مرتب کنیم و این ترتیب هنگام جدا کردن نقاط برحسب x شان تغییر نکند، می توانیم ساختارهای مرتبط با هریک از درخت ها را در زمان خطی بسازیم. این راه، زمان ساخته شدن درخت محدودهٔ دوبعدی را به ( O ( n logn کاهش می دهد، که همچنین زمان ساخت درخت محدوده d بعدی نیز به مرتبهٔ ( O ( n logd−۱n کاهش می یابد.


wiki: درخت محدوده
