درخت سرخ - سیاه متمایل به چپ یکی از انواع درخت های متعادل کننده است. این درخت از زیرشاخه های درخت سرخ - سیاه است. در این درخت گره سرخ تنها می تواند فرزند سمت چپ باشد، به همین دلیل به آن درخت سرخ - سیاه متمایل به چپ می گویند.
درخت سرخ - سیاه متمایل به چپ یک درخت جستجوی دودویی است که ویژگی های زیر را دارد:
• گره می تواند رنگ سرخ یا رنگ سیاه داشته باشد.
• ریشه همیشه رنگ سیاه دارد.
• برگ ها ( که همیشه گره تهی هستند ) رنگ سیاه دارند.
• همه مسیرها از هر گره به همه نوادگانش به تعداد یکسان گره سیاه دارد.
درخت سرخ - سیاه متمایل به چپ دارای دو نوع ارتفاع است:
• ارتفاع معمولی: اندازه طولانی ترین مسیر از برگ ها تا ریشه که معمولاً با h نشان داده می شود.
• ارتفاع سیاه هر گره: ارتفاع سیاه برای گره x برابر است با تعداد گره های سیاه از گره x به نوادگان برگی اش با احتساب رنگ برگ و عدم احتساب رنگ خود x، که معمولاً با bh نشان داده می شود.
قضیه در درخت سرخ - سیاه با n راس روابط زیر برقرار است:
• h ≤ 2 ∗ l o g ( n + 1 ) . {\displaystyle h\leq 2*log ( n+1 ) . }
• b h ≤ l o g ( n + 1 ) . {\displaystyle bh\leq log ( n+1 ) . }
• h ≤ 2 ∗ b h . {\displaystyle h\leq 2*bh. }
طبق قضیه بالا ارتفاع درخت سرخ - سیاه از مرتبه l o g ( n ) است. در نتیجه تمام اعمال اصلی در آن از مرتبه l o g ( n ) انجام می شود.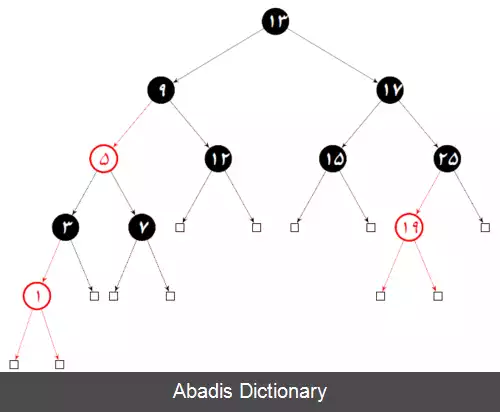
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدرخت سرخ - سیاه متمایل به چپ یک درخت جستجوی دودویی است که ویژگی های زیر را دارد:
• گره می تواند رنگ سرخ یا رنگ سیاه داشته باشد.
• ریشه همیشه رنگ سیاه دارد.
• برگ ها ( که همیشه گره تهی هستند ) رنگ سیاه دارند.
• همه مسیرها از هر گره به همه نوادگانش به تعداد یکسان گره سیاه دارد.
درخت سرخ - سیاه متمایل به چپ دارای دو نوع ارتفاع است:
• ارتفاع معمولی: اندازه طولانی ترین مسیر از برگ ها تا ریشه که معمولاً با h نشان داده می شود.
• ارتفاع سیاه هر گره: ارتفاع سیاه برای گره x برابر است با تعداد گره های سیاه از گره x به نوادگان برگی اش با احتساب رنگ برگ و عدم احتساب رنگ خود x، که معمولاً با bh نشان داده می شود.
قضیه در درخت سرخ - سیاه با n راس روابط زیر برقرار است:
• h ≤ 2 ∗ l o g ( n + 1 ) . {\displaystyle h\leq 2*log ( n+1 ) . }
• b h ≤ l o g ( n + 1 ) . {\displaystyle bh\leq log ( n+1 ) . }
• h ≤ 2 ∗ b h . {\displaystyle h\leq 2*bh. }
طبق قضیه بالا ارتفاع درخت سرخ - سیاه از مرتبه l o g ( n ) است. در نتیجه تمام اعمال اصلی در آن از مرتبه l o g ( n ) انجام می شود.

