در علوم کامپیوتر، درخت دکارتی یک درخت دودویی است که از یک دنباله از اعداد به دست می آید. این درخت به صورت یک هرم می باشد و پیمایش میان ترتیب آن دنبالهٔ اصلی را به دست می د هد. این درخت به صورت یکتا روی هر دنباله قابل تعریف است. این داده ساختار اولین بار در سال ۱۹۸۰ توسط Vuillemin در زمینهٔ داده ساختارهای جستجوی کران معرفی شد. درخت دکارتی همچنین در تعریف داده ساختارهای تیریپ و درخت دودویی جستجوی تصادفی به منظور جستجوی دودویی نیز استفاده شده است. درخت دکارتی با یک الگوریتم پشته محور، به منظور پیدا کردن نزدیک ترین ارقام کوچک تر، در زمان خطی برای یک دنباله از اعداد ساخته می شود.
درخت دکارتی روی یک دنبالهٔ متمایز از اعداد توسط اطلاعات زیر به صورت یکتا تعریف می شود:
• یک درخت دکارتی برای هر عدد در دنباله یک گره دارد. هر گره فقط به یکی از اعداد دنباله نسبت داده می شود.
• یک پیمایش متقارن ( میان ترتیب ) روی این درخت دنبالهٔ اصلی را تولید می کند. در این درخت، زیر درخت سمت چپ زودتر در دنباله ظاهر می شود و این ترتیب در همهٔ گره های این درخت برقرار است.
• این درخت خواص یک هرم را دارد، به این ترتیب که پدر هر گره ( به غیر از ریشه ) از فرزندانش کوچک تر است.
بر اساس خواص هرم، ریشهٔ درخت باید عضو کمینهٔ دنباله باشد؛ بنابراین درخت همچنین می تواند به صورت بازگشتی این چنین تعریف شود که ریشه کمینهٔ دنباله است و زیر درخت های سمت چپ و راست هر کدام درخت های دکارتی مجزایی روی دنباله های سمت چپ و راست ریشه تعریف می شوند؛ بنابراین سه خاصیت بالا درخت دکارتی را به صورت یکتا به دست می دهد. اگر در یک دنباله تکرار داشته باشیم، برای به دست آوردن درخت دکارتی متناظر نیاز به گذاشتن یک قید اضافی ( به طور مثال از بین دو عدد برابر، عددی که زودتر دیده شود به عنوان عدد کوچکتر در نظر گرفته شود ) نیاز داریم. [ ۱]
درخت دکارتی می تواند به عنوان بخشی از داده ساختارهای کارآمد برای پرسمان های کمینهٔ کران و مسئله های جستجوی کران که در بر گیرندهٔ پرسمان هایی برای یافتن مقدار کمینه در یک زیر دنبالهٔ پیوسته از دنبالهٔ اصلی است، می باشد. [ ۲] در یک درخت دکارتی، این مقدار کمینه می تواند جد مشترک راست ترین و چپ ترین مقادیر در زیر دنبالهٔ مورد نظر باشد. به عنوان مثال، در زیردنبالهٔ ( ۱۵، ۲۰، ۱۰، ۱۲ ) در دنبالهٔ مثال زده شده در شکل ( ۱ ) ، مقدار کمینه ( ۱۰ ) ، پایین ترین جد مشترک راست ترین و چپ ترین مقادیر زیردنباله ( ۱۲ و ۱۵ ) می باشد. به دلیل این که پایین ترین جد مشترک به ازای هر پرسمان در زمان ثابتی به دست می آید، استفاده از داده ساختاری که حجم خطی اشغال می کند و در زمان خطی ساخته می شود، [ ۳] باعث می شود مسئلهٔ کمینه کردن کران نیز محدود به همین مرزها شود.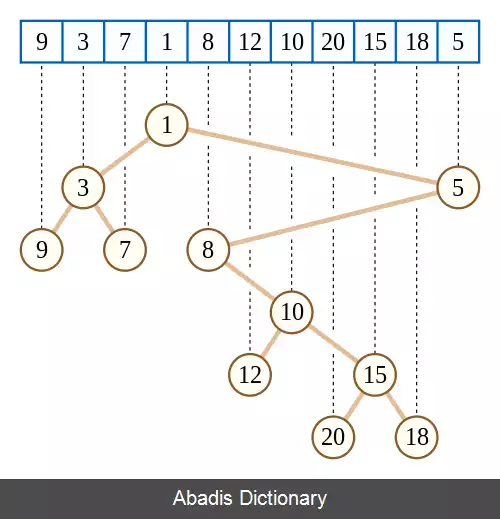
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدرخت دکارتی روی یک دنبالهٔ متمایز از اعداد توسط اطلاعات زیر به صورت یکتا تعریف می شود:
• یک درخت دکارتی برای هر عدد در دنباله یک گره دارد. هر گره فقط به یکی از اعداد دنباله نسبت داده می شود.
• یک پیمایش متقارن ( میان ترتیب ) روی این درخت دنبالهٔ اصلی را تولید می کند. در این درخت، زیر درخت سمت چپ زودتر در دنباله ظاهر می شود و این ترتیب در همهٔ گره های این درخت برقرار است.
• این درخت خواص یک هرم را دارد، به این ترتیب که پدر هر گره ( به غیر از ریشه ) از فرزندانش کوچک تر است.
بر اساس خواص هرم، ریشهٔ درخت باید عضو کمینهٔ دنباله باشد؛ بنابراین درخت همچنین می تواند به صورت بازگشتی این چنین تعریف شود که ریشه کمینهٔ دنباله است و زیر درخت های سمت چپ و راست هر کدام درخت های دکارتی مجزایی روی دنباله های سمت چپ و راست ریشه تعریف می شوند؛ بنابراین سه خاصیت بالا درخت دکارتی را به صورت یکتا به دست می دهد. اگر در یک دنباله تکرار داشته باشیم، برای به دست آوردن درخت دکارتی متناظر نیاز به گذاشتن یک قید اضافی ( به طور مثال از بین دو عدد برابر، عددی که زودتر دیده شود به عنوان عدد کوچکتر در نظر گرفته شود ) نیاز داریم. [ ۱]
درخت دکارتی می تواند به عنوان بخشی از داده ساختارهای کارآمد برای پرسمان های کمینهٔ کران و مسئله های جستجوی کران که در بر گیرندهٔ پرسمان هایی برای یافتن مقدار کمینه در یک زیر دنبالهٔ پیوسته از دنبالهٔ اصلی است، می باشد. [ ۲] در یک درخت دکارتی، این مقدار کمینه می تواند جد مشترک راست ترین و چپ ترین مقادیر در زیر دنبالهٔ مورد نظر باشد. به عنوان مثال، در زیردنبالهٔ ( ۱۵، ۲۰، ۱۰، ۱۲ ) در دنبالهٔ مثال زده شده در شکل ( ۱ ) ، مقدار کمینه ( ۱۰ ) ، پایین ترین جد مشترک راست ترین و چپ ترین مقادیر زیردنباله ( ۱۲ و ۱۵ ) می باشد. به دلیل این که پایین ترین جد مشترک به ازای هر پرسمان در زمان ثابتی به دست می آید، استفاده از داده ساختاری که حجم خطی اشغال می کند و در زمان خطی ساخته می شود، [ ۳] باعث می شود مسئلهٔ کمینه کردن کران نیز محدود به همین مرزها شود.



wiki: درخت دکارتی
