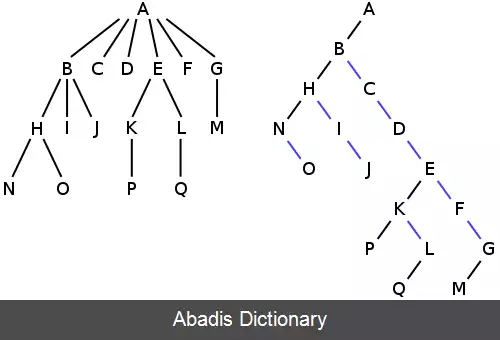
درخت دودویی فرزند چپ همزاد راست ( به انگلیسی: Left - child right - sibling binary tree ) ( اختصاری LC - RS ) در علوم رایانه، یک درخت باینری است که بازنمایی ای از درخت K تایی ( به انگلیسی: k - ary tree ) است. [ ۱] روش تبدیل یک درخت K تایی دلخواه به یک درخت باینری به این صورت است که، ریشه درخت اولیه به عنوان ریشه درخت باینری در نظر گرفته می شود. سپس از ریشه شروع می کنیم و سمت چپ ترین فرزند هر رأس در درخت اولیه، فرزند چپ آن رأس در درخت باینری را می سازد و نزدیک ترین همزاد راست در درخت اولیه، فرزند راست درخت باینری را می سازد. [ ۲] اگر درخت اولیه مرتب شده باشد، درخت جدید درخت جستجوی دودویی خواهد بود.
درخت G یک گراف ساده بدون جهت است که در یکی از شروط معادل زیر صدق کند:[ ۳]
• G {\displaystyle G} همبند است و دور ندارد.
• G {\displaystyle G} هیج دوری ندارد و اگر یک یال به آن اضافه شود یک دور ساده در آن به وجود می آید.
• G {\displaystyle G} همبند است و اگر یک یال آن حذف شود دیگر متصل نیست.
• G {\displaystyle G} همبند است و گراف کامل ۳ رأسی K 3 {\displaystyle K_{3}} جزِئی از آن نیست.
• هر دو رأس در G {\displaystyle G} با یک مسیر سادهٔ یکتا به هم وصل می شوند.
اگر G تعداد متناهی رأس داشته باشد احکام بالا با شروط زیر نیز معادل اند:
• G {\displaystyle G} همبند است و n − 1 {\displaystyle n - 1} یال دارد.
• G {\displaystyle G} دور ساده ندارد و n − 1 {\displaystyle n - 1} یال دارد.
برای بررسی یک درخت ابتدا یک رأس مانند رأس V را انتخاب کرده و آن را به عنوان ریشه درخت در نظر می گیریم. حال اگر دو رأس مانند T , E به هم با یک یال متصل باشند با استفاده از تعریف فاصله که بیان می کند فاصله دو رأس از یک دیگر به میزان تعداد یال های کوتاه ترین مسیر بین آن دو رأس است ( که با توجه به درخت بودن گراف مطمئن هستیم مسیر وجود دارد ) تعریف می کنیم رأسی که فاصله کمتری تا رأس V که رأس ریشه است دارد پدر رأس دیگر است و دیگری فرزند آن به حساب می آید. برای مثال داریم:
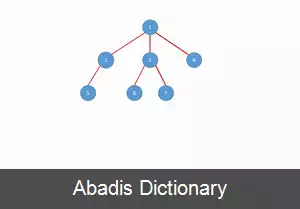
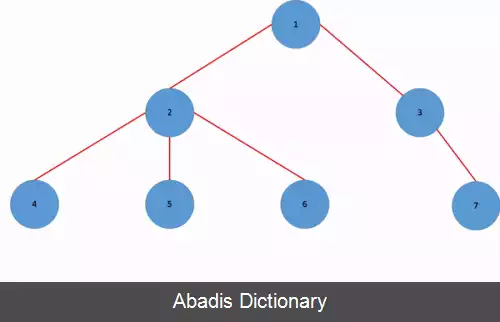
۱ / \ / \ ۲ ۳ / \ / \ ۴ ۵ در این شکل ۱ به عنوان ریشه انتخاب شده است، ۲ و ۳ فرزندان ۱ هستند، ۲ فرزندی ندارد و ۴ و ۵ فرزندان ۳ هستند. این درخت را به گونه ای دیگر نیز می توان نشان داد.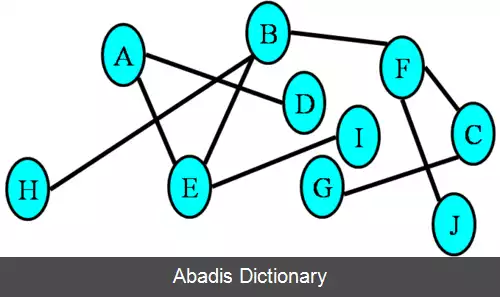
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدرخت G یک گراف ساده بدون جهت است که در یکی از شروط معادل زیر صدق کند:[ ۳]
• G {\displaystyle G} همبند است و دور ندارد.
• G {\displaystyle G} هیج دوری ندارد و اگر یک یال به آن اضافه شود یک دور ساده در آن به وجود می آید.
• G {\displaystyle G} همبند است و اگر یک یال آن حذف شود دیگر متصل نیست.
• G {\displaystyle G} همبند است و گراف کامل ۳ رأسی K 3 {\displaystyle K_{3}} جزِئی از آن نیست.
• هر دو رأس در G {\displaystyle G} با یک مسیر سادهٔ یکتا به هم وصل می شوند.
اگر G تعداد متناهی رأس داشته باشد احکام بالا با شروط زیر نیز معادل اند:
• G {\displaystyle G} همبند است و n − 1 {\displaystyle n - 1} یال دارد.
• G {\displaystyle G} دور ساده ندارد و n − 1 {\displaystyle n - 1} یال دارد.
برای بررسی یک درخت ابتدا یک رأس مانند رأس V را انتخاب کرده و آن را به عنوان ریشه درخت در نظر می گیریم. حال اگر دو رأس مانند T , E به هم با یک یال متصل باشند با استفاده از تعریف فاصله که بیان می کند فاصله دو رأس از یک دیگر به میزان تعداد یال های کوتاه ترین مسیر بین آن دو رأس است ( که با توجه به درخت بودن گراف مطمئن هستیم مسیر وجود دارد ) تعریف می کنیم رأسی که فاصله کمتری تا رأس V که رأس ریشه است دارد پدر رأس دیگر است و دیگری فرزند آن به حساب می آید. برای مثال داریم:
۱ / \ / \ ۲ ۳ / \ / \ ۴ ۵ در این شکل ۱ به عنوان ریشه انتخاب شده است، ۲ و ۳ فرزندان ۱ هستند، ۲ فرزندی ندارد و ۴ و ۵ فرزندان ۳ هستند. این درخت را به گونه ای دیگر نیز می توان نشان داد.




