در علوم رایانه، یک درخت دودویی یک ساختمان دادهٔ درخت است که در آن هر گره حداکثر دو گره فرزند دارد که فرزندان راست و چپ نامیده می شوند. در درخت دودویی، در جهٔ هر گره حداکثر می تواند دو باشد. درخت های دودویی برای پیاده سازی درخت جستجوی دودویی و انبوه دودویی و برای جستجوی کارآمد و مرتب سازی استفاده می شود. درخت دودویی یک حالت خاص از یک درخت kتایی است، که در آن k برابر ۲ است.
• درخت دودویی ریشه دار یک درخت با یک گره ریشه است که در آن هر گره حداکثر دو فرزند دارد.
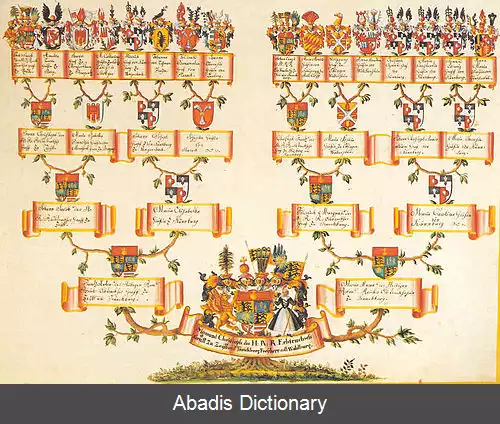
• درخت دودویی پر ( گاهی درخت دودویی مناسب یا ۲_ درخت یا درخت اکیداً دودویی گفته می شود ) یک درخت که در آن هر گره به غیر از برگ ها دارای دو فرزند است. هر گره در درخت دودویی دارای دو فرزند یا بدون فرزند است. یک درخت پر گاهی به طور ابهام انگیزی به عنوان درخت دودویی کامل تعریف می شود. فیزیکدانان یک درخت دودویی را به عنوان درخت دودویی پر تعریف می کنند. [ ۱] یک تبارنامه که روی یک درخت دودویی کامل به عمق ۴ نگاشت شده است
• یک درخت دودویی کامل ( perfect ) یک درخت دودویی پر است که در آن همه برگ ها دارای عمق یکسان یا هم سطح باشند، و در آن هر پدری دارای دو فرزند است. [ ۲] ( به طور مبهم درخت دودویی کامل نامیده می شود ( بعدی را مشاهده کنید ) . ) نمونه ای از یک درخت دودویی کامل را می توان در تبارنامه از یک فرد به عمق داده شده مشاهده کرد، به طوری که هر فرد دقیقاً دو پدر و مادر ( یک مادر و یک پدر ) دارد؛ توجه داشته باشید که این معکوس قرارداد معمول درخت پدر\ فرزند است، و این درختان خلاف جهت معمول هستند ( ریشه در پایین ) .
• یک درخت دودویی کامل ( complete ) یک درخت دودویی است که در آن هر سطح، به جز احتمالاً آخرین سطح، به طور کامل پر شده است، و همهٔ گره ها تا جایی که ممکن است در چپ درخت قرار می گیرند. [ ۳] درختی که این استثناء را داشته باشد که سطح آخر آن کاملاً پر نباشد، درخت دودویی تقریباً کامل یا نزدیک به درخت دودویی کامل گویند. این نوع درختان از ساختمان دادهٔ ویژه ای به نام هیپ استفاده می کنند.
• درخت دودویی کامل نا محدود درختی است که دارای بی نهایت سطح قابل شمارش است، که در آن هر گره دارای دو فرزند است به طوری که گره های 2d در سطح d هستند. مجموعهٔ گره ها شمارای نامتناهی است، ولی مجموعه ای از بی نهایت مسیر از ریشه، ناشمارا است، که دارای عدد کاردینالیتی پیوسته است. این مسیرها رابطهٔ دوسویی را با نقاط مجموعه کانتور، یا مجموعه ای از اعداد گنگ حفظ می کند.
• درختی دودویی متوازن که معمولاً به عنوان درخت دودویی است که در آن اختلاف عمق زیردرخت چپ و راست آن ۱ یا کمتر است، اگر چه به طور کلی درخت دودویی است که هیچ برگی نسبت با برگ های دیگر فاصلهٔ زیادی تا ریشه ندارد. ( طرح توازن متمایز اجازه می دهد که تعریف متفاوتی از «بسیار دورتر» ارائه شود ) درخت دودویی هنگامی متوازن است که مطابق تعریف عمق آن قابل پیش بینی باشد. ( بسیاری از گره ها از ریشه تا برگ پیموده می شوند، چنان که شمارهٔ ریشه به عنوان گرهٔ ۰ و بقیهٔ گره ها اعداد ۱ ۲ … n را می گیرند ) این عمق ( ارتفاع هم نامیده می شود ) برابر قسمت صحیح ( log2 ( n است، که در آن n تعداد گره ها در درخت متوازن است؛ مثلاً، برای درخت متوازنی که دارای ۱ گره است، log2 ( 1 ) = ۰، در نتیجه عمق درخت برابر صفر است. برای یک درخت متوازن با ۱۰۰ گره، log2 ( 100 ) = ۶٫۶۴، در نتیجه عمق درخت برابر ۶ است.
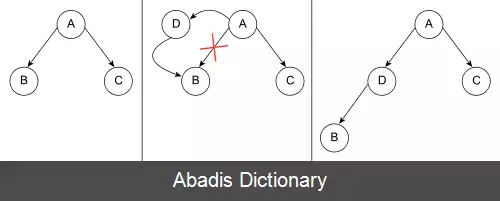
• درخت منحط درختی است که هر گرهٔ والدین فقط به یک گرهٔ فرزند متصل است. این به این معنی است که عملکرد این درخت مانند رفتار ساختمان دادهٔ لیست پیوندی است.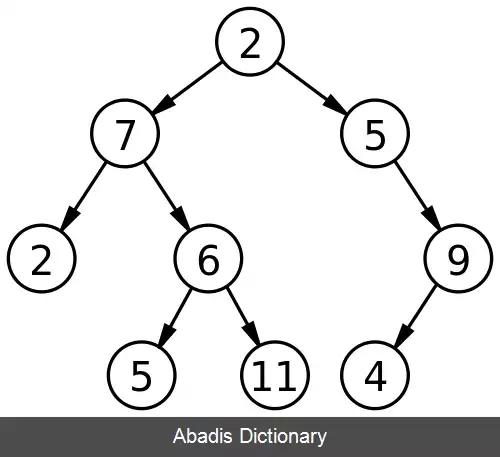
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• درخت دودویی ریشه دار یک درخت با یک گره ریشه است که در آن هر گره حداکثر دو فرزند دارد.
• درخت دودویی پر ( گاهی درخت دودویی مناسب یا ۲_ درخت یا درخت اکیداً دودویی گفته می شود ) یک درخت که در آن هر گره به غیر از برگ ها دارای دو فرزند است. هر گره در درخت دودویی دارای دو فرزند یا بدون فرزند است. یک درخت پر گاهی به طور ابهام انگیزی به عنوان درخت دودویی کامل تعریف می شود. فیزیکدانان یک درخت دودویی را به عنوان درخت دودویی پر تعریف می کنند. [ ۱] یک تبارنامه که روی یک درخت دودویی کامل به عمق ۴ نگاشت شده است
• یک درخت دودویی کامل ( perfect ) یک درخت دودویی پر است که در آن همه برگ ها دارای عمق یکسان یا هم سطح باشند، و در آن هر پدری دارای دو فرزند است. [ ۲] ( به طور مبهم درخت دودویی کامل نامیده می شود ( بعدی را مشاهده کنید ) . ) نمونه ای از یک درخت دودویی کامل را می توان در تبارنامه از یک فرد به عمق داده شده مشاهده کرد، به طوری که هر فرد دقیقاً دو پدر و مادر ( یک مادر و یک پدر ) دارد؛ توجه داشته باشید که این معکوس قرارداد معمول درخت پدر\ فرزند است، و این درختان خلاف جهت معمول هستند ( ریشه در پایین ) .
• یک درخت دودویی کامل ( complete ) یک درخت دودویی است که در آن هر سطح، به جز احتمالاً آخرین سطح، به طور کامل پر شده است، و همهٔ گره ها تا جایی که ممکن است در چپ درخت قرار می گیرند. [ ۳] درختی که این استثناء را داشته باشد که سطح آخر آن کاملاً پر نباشد، درخت دودویی تقریباً کامل یا نزدیک به درخت دودویی کامل گویند. این نوع درختان از ساختمان دادهٔ ویژه ای به نام هیپ استفاده می کنند.
• درخت دودویی کامل نا محدود درختی است که دارای بی نهایت سطح قابل شمارش است، که در آن هر گره دارای دو فرزند است به طوری که گره های 2d در سطح d هستند. مجموعهٔ گره ها شمارای نامتناهی است، ولی مجموعه ای از بی نهایت مسیر از ریشه، ناشمارا است، که دارای عدد کاردینالیتی پیوسته است. این مسیرها رابطهٔ دوسویی را با نقاط مجموعه کانتور، یا مجموعه ای از اعداد گنگ حفظ می کند.
• درختی دودویی متوازن که معمولاً به عنوان درخت دودویی است که در آن اختلاف عمق زیردرخت چپ و راست آن ۱ یا کمتر است، اگر چه به طور کلی درخت دودویی است که هیچ برگی نسبت با برگ های دیگر فاصلهٔ زیادی تا ریشه ندارد. ( طرح توازن متمایز اجازه می دهد که تعریف متفاوتی از «بسیار دورتر» ارائه شود ) درخت دودویی هنگامی متوازن است که مطابق تعریف عمق آن قابل پیش بینی باشد. ( بسیاری از گره ها از ریشه تا برگ پیموده می شوند، چنان که شمارهٔ ریشه به عنوان گرهٔ ۰ و بقیهٔ گره ها اعداد ۱ ۲ … n را می گیرند ) این عمق ( ارتفاع هم نامیده می شود ) برابر قسمت صحیح ( log2 ( n است، که در آن n تعداد گره ها در درخت متوازن است؛ مثلاً، برای درخت متوازنی که دارای ۱ گره است، log2 ( 1 ) = ۰، در نتیجه عمق درخت برابر صفر است. برای یک درخت متوازن با ۱۰۰ گره، log2 ( 100 ) = ۶٫۶۴، در نتیجه عمق درخت برابر ۶ است.
• درخت منحط درختی است که هر گرهٔ والدین فقط به یک گرهٔ فرزند متصل است. این به این معنی است که عملکرد این درخت مانند رفتار ساختمان دادهٔ لیست پیوندی است.






wiki: درخت دودویی
