درخت جستجوی دودویی متوازن وزن دار نوعی خاص از درخت جستجوی دودویی است. این درخت با دانستن احتمال جستجوی هر گره، متوازن می گردد. احتمال مورد جستجو قرار گرفتن هر گره، وزن آن گره نامیده می شود. در هر زیردرخت گره ای که بیشترین وزن را دارد به عنوان ریشه در نظر گرفته می شود. بر این اساس سرعت جستجو بهبود پیدا می کند.
ساخت این درخت بسیار شبیه به داده ساختار تیریپ است؛ با این تفاوت که وزن گره ها به جای آن که به صورت تصادفی انتخاب گردد، بر اساس احتمال مورد جستجو قرار گرفتن تعیین می گردد.
در یک درخت جستجوی دودویی متوازن وزن دار با n گره، امید ریاضی طول جستجوی موفق، به مقدار بهینه لگاریتمی ( log ( n نزدیک است. در درختی که در تصویر مشاهده می گردد، این مقدار چنین محاسبه می شود:
امید ریاضی طول جستجوی موفق = احتمال جستجوی گره A * عمق گره A + احتمال جستجوی گره C * عمق گره C + . . .
۲. ۵ = ۰. ۱۷ * ۲ + ۰. ۰۳ * ۵ + ۰. ۰۹ * ۴ + ۰. ۱۲ * ۳ + ۰. ۲۰ * ۱ + ۰. ۱۱ * ۳ + ۰. ۱۰ * ۳ + ۰. ۱۸ * ۲
در نهایت، مقدار به دست آمده، میانگین تعداد نقاطی را نشان می دهد که در یک جستجوی موفق مورد وارسی قرار می گیرند.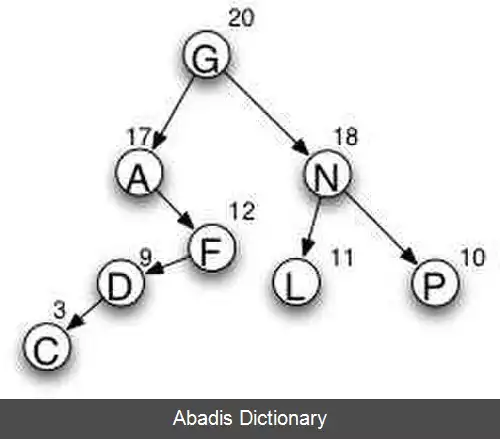
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفساخت این درخت بسیار شبیه به داده ساختار تیریپ است؛ با این تفاوت که وزن گره ها به جای آن که به صورت تصادفی انتخاب گردد، بر اساس احتمال مورد جستجو قرار گرفتن تعیین می گردد.
در یک درخت جستجوی دودویی متوازن وزن دار با n گره، امید ریاضی طول جستجوی موفق، به مقدار بهینه لگاریتمی ( log ( n نزدیک است. در درختی که در تصویر مشاهده می گردد، این مقدار چنین محاسبه می شود:
امید ریاضی طول جستجوی موفق = احتمال جستجوی گره A * عمق گره A + احتمال جستجوی گره C * عمق گره C + . . .
۲. ۵ = ۰. ۱۷ * ۲ + ۰. ۰۳ * ۵ + ۰. ۰۹ * ۴ + ۰. ۱۲ * ۳ + ۰. ۲۰ * ۱ + ۰. ۱۱ * ۳ + ۰. ۱۰ * ۳ + ۰. ۱۸ * ۲
در نهایت، مقدار به دست آمده، میانگین تعداد نقاطی را نشان می دهد که در یک جستجوی موفق مورد وارسی قرار می گیرند.

