در علوم رایانه یک درخت درخت جستجوی دودویی خود - متوازن, هر درخت جستجوی دودویی گره - محور است که به طور خودکار ارتفاعش را ( حداکثر تعداد مراحل زیر ریشه ) در درج و حذف عنصر دلخواه، کوچک نگه می دارد. این ساختارها اجراهای مؤثری برای لیست های مرتب تغییر ناپذیر به وجود می آورد و می تواند به عنوان نوع داده انتزاعی چون آرایه انجمنی, صف اولویت دار و مجموعه ها، مورد استفاده قرار گیرد.
بیشتر عملیات روی یک درخت جستجوی دودویی ( ددج ) , زمانی مستقیماً متناسب با ارتفاع درخت می برند. پس مطلوب است که ارتفاع را کوچک نگه داریم. یک درخت دودویی با ارتفاع h می تواند شامل حداکثر 20+21+···+2h = 2h+1− ۱ گره باشد. بنابراین برای درختی با n گره و ارتفاع h داریم: n ≤ 2 h + 1 − 1 و این دلالت دارد بر اینکه: h ≥ ⌈ log 2 ( n + 1 ) − 1 ⌉ ≥ ⌊ log 2 n ⌋ .
به بیان دیگر حداقل ارتفاع یک درخت با n گره برابر است با log2 ( n ) با روند کردن رو به پایین داریم: ⌊ log 2 n ⌋
هرچند ساده ترین الگوریتم برای درج عنصر در ددج، ممکن است یک درخت با ارتفاع n را در حالتهای مشترک نتیجه دهد. برای مثال وقتی عناصر در ترتیب مرتب شدهٔ کلیدها درج می شوند، درخت به یک لیست پیوندی با n گره تبدیل می شود. اختلاف کارایی این دو موقعیت ممکن است خیلی زیاد باشد. برای مثال برای n=۱٬۰۰۰٬۰۰۰ حداقل ارتفاع برابر است با: ⌊ log 2 ( n ) ⌋ = 19 .
اگر این آیتم های داده شده پیش از زمان شناخته شوند، به طور متوسط با اضافه کردن مقادیر در ترتیب تصادفی که یک درخت جستجوی دودویی را نتیجه می دهد، می توان ارتفاع درخت را همچنان کوچک نگه داشت. هرچند موقعیت های بسیاری ( همانند الگوریتم های برخط ) که این تصادفی کردن غیرقابل دوام است. درخت های دودویی خود متوازن این مسئله را با اعمال تغییراتی بر روی درخت ( همانند چرخش درخت ) در زمان های کلیدی به منظور نگه داشتن ارتفاع متناسب با log2 ( n ) , حداقل کرده اند. اگرچه یک سربار درگیر باشد، ممکن است در مدت زمان اجرای طولانی با اطمینان حاصل کردن از سریع اجرا شدن عملیات بعدی، توجیه شده باشد. نگه داشتن درخت در حداقل مقدار آن ⌊ log 2 ( n ) ⌋ همیشه دوام پذیر نیست. می شود ثابت کرد که هر الگوریتم درج که قبلاً همانند آن را انجام دادیم، یک سربار بیش از اندازه خواهد داشت. از این رو بیشتر الگوریتم های ددج خود - متوازن، ارتفاع را تا یک ضریبی از کران پایین، ثابت نگه می دارند. در کران بالای مجانبی ( O بزرگ ) یک ساختار ددج خود متوازن که شامل n عنصر است, اجازهٔ وارسی، درج و حذف یک عنصر را در بدترین زمان اجرای ( O ( log n و در پیمایش درخت روی همهٔ عناصر در زمان ( O ( n می دهد. برای بعضی از اجراها، این ها کران های زمان در - عمل هستند. در صورتی که برای بقیه، آن ها کران های مستهلک بیش از یک دنباله از عملیات هستند. این زمان ها، به طور مجانبی برای همهٔ سختمان داده هایی که کلیدها را فقط در مقایسه دستکاری می کنند، بهینه هستند.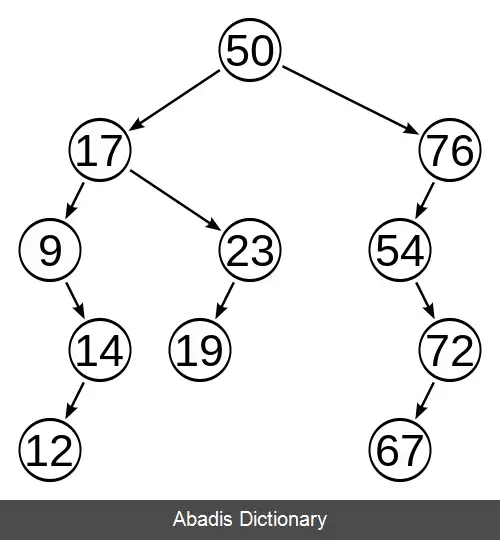
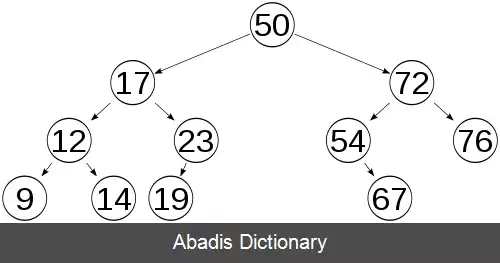
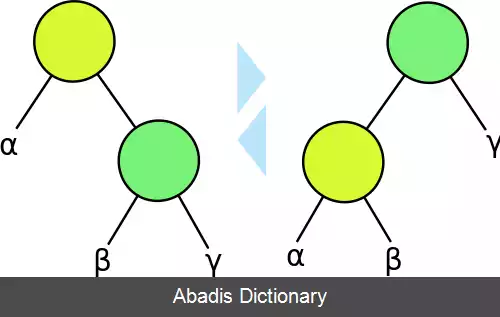
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبیشتر عملیات روی یک درخت جستجوی دودویی ( ددج ) , زمانی مستقیماً متناسب با ارتفاع درخت می برند. پس مطلوب است که ارتفاع را کوچک نگه داریم. یک درخت دودویی با ارتفاع h می تواند شامل حداکثر 20+21+···+2h = 2h+1− ۱ گره باشد. بنابراین برای درختی با n گره و ارتفاع h داریم: n ≤ 2 h + 1 − 1 و این دلالت دارد بر اینکه: h ≥ ⌈ log 2 ( n + 1 ) − 1 ⌉ ≥ ⌊ log 2 n ⌋ .
به بیان دیگر حداقل ارتفاع یک درخت با n گره برابر است با log2 ( n ) با روند کردن رو به پایین داریم: ⌊ log 2 n ⌋
هرچند ساده ترین الگوریتم برای درج عنصر در ددج، ممکن است یک درخت با ارتفاع n را در حالتهای مشترک نتیجه دهد. برای مثال وقتی عناصر در ترتیب مرتب شدهٔ کلیدها درج می شوند، درخت به یک لیست پیوندی با n گره تبدیل می شود. اختلاف کارایی این دو موقعیت ممکن است خیلی زیاد باشد. برای مثال برای n=۱٬۰۰۰٬۰۰۰ حداقل ارتفاع برابر است با: ⌊ log 2 ( n ) ⌋ = 19 .
اگر این آیتم های داده شده پیش از زمان شناخته شوند، به طور متوسط با اضافه کردن مقادیر در ترتیب تصادفی که یک درخت جستجوی دودویی را نتیجه می دهد، می توان ارتفاع درخت را همچنان کوچک نگه داشت. هرچند موقعیت های بسیاری ( همانند الگوریتم های برخط ) که این تصادفی کردن غیرقابل دوام است. درخت های دودویی خود متوازن این مسئله را با اعمال تغییراتی بر روی درخت ( همانند چرخش درخت ) در زمان های کلیدی به منظور نگه داشتن ارتفاع متناسب با log2 ( n ) , حداقل کرده اند. اگرچه یک سربار درگیر باشد، ممکن است در مدت زمان اجرای طولانی با اطمینان حاصل کردن از سریع اجرا شدن عملیات بعدی، توجیه شده باشد. نگه داشتن درخت در حداقل مقدار آن ⌊ log 2 ( n ) ⌋ همیشه دوام پذیر نیست. می شود ثابت کرد که هر الگوریتم درج که قبلاً همانند آن را انجام دادیم، یک سربار بیش از اندازه خواهد داشت. از این رو بیشتر الگوریتم های ددج خود - متوازن، ارتفاع را تا یک ضریبی از کران پایین، ثابت نگه می دارند. در کران بالای مجانبی ( O بزرگ ) یک ساختار ددج خود متوازن که شامل n عنصر است, اجازهٔ وارسی، درج و حذف یک عنصر را در بدترین زمان اجرای ( O ( log n و در پیمایش درخت روی همهٔ عناصر در زمان ( O ( n می دهد. برای بعضی از اجراها، این ها کران های زمان در - عمل هستند. در صورتی که برای بقیه، آن ها کران های مستهلک بیش از یک دنباله از عملیات هستند. این زمان ها، به طور مجانبی برای همهٔ سختمان داده هایی که کلیدها را فقط در مقایسه دستکاری می کنند، بهینه هستند.



