در علوم رایانه، درخت جستجوی دودویی ( به انگلیسی: Binary search tree یا به اختصار BST ) که گاهی درخت دودویی مرتب هم نامیده می شود، یک ساختار داده است و نوعی درخت دودویی است.
یک درخت باینری نوعی ساختارداده برای ذخیره کردن داده است مانند عددهاییی که مرتب شده هستند. درخت جست و جوی دودویی این امکان را فراهم می کند که جست و جوی یک عدد، اضافه کردن آن و حذف کردن آن با سرعت بیشتری انجام شود. همچنین این امکان را فراهم می کند که مجموعه های پویا و جداول جست و جو را پیاده سازی کنیم.
ترتیب گره ها در دخت جست و جوی دودویی به صورتی است که در هر مقایسه نیمی از درخت باقی مانده بررسی نمی شود؛ بنابراین زمان جست و جوی درخت متناسب با لگاریتم تعداد عددهای ذخیره شده در درخت است. این زمان بسیار کمتر از زمان جست و جوی خطی در یک آرایه مرتب نشده است اما کندتر از انجام عملیات درهم سازی است.
انواع مختلفی از درخت های جست و جوی دودویی مورد بررسی و مطالعه قرار گرفته اند.
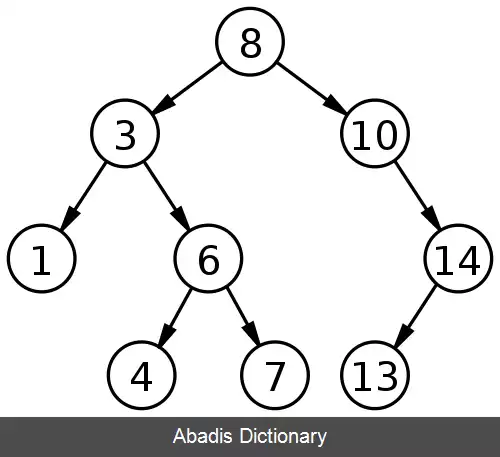
درخت جستجوی دودویی، نوعی درخت دودویی است که ممکن است تهی باشد، اگر تهی نباشد، دارای خصوصیات زیر است:
• از تعدادی گره تشکیل شده که هر گره دارای یک کلید است. کلیدها منحصربه فرد هستند و در درخت کلید تکراری وجود ندارد.
• تمام کلیدهایی که در زیردرخت سمت چپ واقع شده اند، کوچکتر از کلید گره ریشه هستند.
• تمام کلیدهایی که در زیردرخت سمت راست واقع شده اند، بزرگتر از کلید گره ریشه هستند.
• زیردرخت سمت راست و زیردرخت سمت چپ خود درختان جستجوی دودویی هستند.
این ویژگی تضمین می کند که پیمایش میان ترتیب یک درخت جستجوی دودویی، کلیدها را به ترتیب صعودی نمایش می دهد.
در ادامه برخی اصطلاح های مهم مربوط به درخت مورد اشاره قرار گرفته است:
• مسیر ( path ) – منظور از مسیر در یک درخت، یک توالی از گره ها در راستای یال های درخت است.
• ریشه ( Root ) – گرهی که در بخش فوقانی درخت قرار دارد، ریشه نامیده می شود. هر درختی تنها یک ریشه دارد و از گره ریشه تنها یک مسیر به هر گره دیگر وجود دارد.
• والد ( parent ) – هر گرهی به جز گره ریشه یالی به سمت بالا به یک گره دارد، که والد آن گره نامیده می شود.
• فرزند ( child ) – گرهی که زیر یک گره مفروض قرار دارد و از طریق یالی به سمت پایین به آن وصل شده است، گره فرزند آن نامیده می شود.
• برگ ( leaf ) – گرهی که هیچ فرزندی دارد، برگ نامیده می شود.
• زیردرخت ( Subtree ) – به مجموعه فرزندان یک گره، زیردرخت گفته می شود.
• بازدید ( Visiting ) – منظور از بازدید، بررسی ارزش یک گره است، هنگامی که کنترل روی گره قرار دارد.
• جست و جوی دودویی روی آرایهٔ مرتب شدهپیمایش ( Traversing ) – منظور از پیمایش، عبور از میان گره های یک درخت با ترتیب خاص است.
• سطوح ( Levels ) – سطح یک گره نماینده نسل آن فرزند است. اگر گره ریشه در سطح ۰ باشد، در این صورت فرزندان آن در سطح ۱، نوه های آن در سطح ۲ و همین طور تا آخر … قرار دارند.
• کلیدها ( Keys ) – کلید نماینده ارزش یک گره بر مبنای نوع عملیات جستجویی است که قرار است روی گره انجام شود.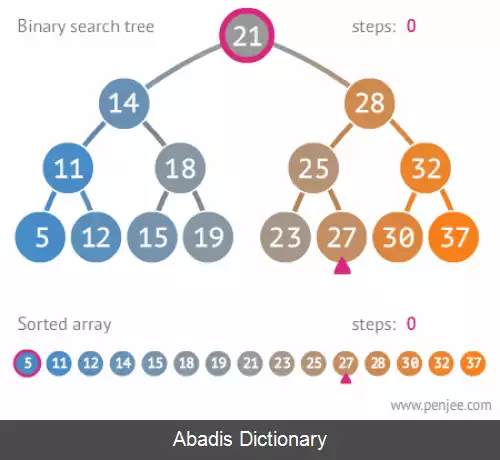

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک درخت باینری نوعی ساختارداده برای ذخیره کردن داده است مانند عددهاییی که مرتب شده هستند. درخت جست و جوی دودویی این امکان را فراهم می کند که جست و جوی یک عدد، اضافه کردن آن و حذف کردن آن با سرعت بیشتری انجام شود. همچنین این امکان را فراهم می کند که مجموعه های پویا و جداول جست و جو را پیاده سازی کنیم.
ترتیب گره ها در دخت جست و جوی دودویی به صورتی است که در هر مقایسه نیمی از درخت باقی مانده بررسی نمی شود؛ بنابراین زمان جست و جوی درخت متناسب با لگاریتم تعداد عددهای ذخیره شده در درخت است. این زمان بسیار کمتر از زمان جست و جوی خطی در یک آرایه مرتب نشده است اما کندتر از انجام عملیات درهم سازی است.
انواع مختلفی از درخت های جست و جوی دودویی مورد بررسی و مطالعه قرار گرفته اند.
درخت جستجوی دودویی، نوعی درخت دودویی است که ممکن است تهی باشد، اگر تهی نباشد، دارای خصوصیات زیر است:
• از تعدادی گره تشکیل شده که هر گره دارای یک کلید است. کلیدها منحصربه فرد هستند و در درخت کلید تکراری وجود ندارد.
• تمام کلیدهایی که در زیردرخت سمت چپ واقع شده اند، کوچکتر از کلید گره ریشه هستند.
• تمام کلیدهایی که در زیردرخت سمت راست واقع شده اند، بزرگتر از کلید گره ریشه هستند.
• زیردرخت سمت راست و زیردرخت سمت چپ خود درختان جستجوی دودویی هستند.
این ویژگی تضمین می کند که پیمایش میان ترتیب یک درخت جستجوی دودویی، کلیدها را به ترتیب صعودی نمایش می دهد.
در ادامه برخی اصطلاح های مهم مربوط به درخت مورد اشاره قرار گرفته است:
• مسیر ( path ) – منظور از مسیر در یک درخت، یک توالی از گره ها در راستای یال های درخت است.
• ریشه ( Root ) – گرهی که در بخش فوقانی درخت قرار دارد، ریشه نامیده می شود. هر درختی تنها یک ریشه دارد و از گره ریشه تنها یک مسیر به هر گره دیگر وجود دارد.
• والد ( parent ) – هر گرهی به جز گره ریشه یالی به سمت بالا به یک گره دارد، که والد آن گره نامیده می شود.
• فرزند ( child ) – گرهی که زیر یک گره مفروض قرار دارد و از طریق یالی به سمت پایین به آن وصل شده است، گره فرزند آن نامیده می شود.
• برگ ( leaf ) – گرهی که هیچ فرزندی دارد، برگ نامیده می شود.
• زیردرخت ( Subtree ) – به مجموعه فرزندان یک گره، زیردرخت گفته می شود.
• بازدید ( Visiting ) – منظور از بازدید، بررسی ارزش یک گره است، هنگامی که کنترل روی گره قرار دارد.
• جست و جوی دودویی روی آرایهٔ مرتب شدهپیمایش ( Traversing ) – منظور از پیمایش، عبور از میان گره های یک درخت با ترتیب خاص است.
• سطوح ( Levels ) – سطح یک گره نماینده نسل آن فرزند است. اگر گره ریشه در سطح ۰ باشد، در این صورت فرزندان آن در سطح ۱، نوه های آن در سطح ۲ و همین طور تا آخر … قرار دارند.
• کلیدها ( Keys ) – کلید نماینده ارزش یک گره بر مبنای نوع عملیات جستجویی است که قرار است روی گره انجام شود.






wiki: درخت جستجوی دودویی
