در علوم کامپیوتر، یک درخت بی یا بی تری ( به انگلیسی: B - tree ) داده ساختاری درختی است که داده ها را به صورت مرتب شده نگه می دارد و جستجو، درج و حذف را در زمان مصرفی لگاریتمی میسر می سازد. برخلاف درخت های جستجوی دودویی متوازن ( به انگلیسی: Balanced binary search tree ) ، این داده ساختار برای سیستم هایی که بلاک های عظیم اطلاعات را خوانده و می نویسند بهینه سازی شده است. این داده ساختار معمولاً در پایگاه های داده و سیستم پرونده استفاده می شود.
در درخت بی، گره های درونی ( و نه برگ ها ) می توانند یک شمارهٔ متغیر از محدوده ای ازپیش تعریف شده مربوط به گره های فرزند را اختیار کنند. زمانی که داده ها درج شده یا از یک گره حذف می شوند، شمارهٔ گره های فرزند آن ها تغییر می کند. به منظور نگه داری محدودهٔ ازپیش تعریف شده، ممکن است گره های درونی به هم متصل شده یا از هم جدا شوند. به دلیل اینکه محدوده ای از گره های فرزند مجاز هستند، درخت بی، همانند دیگر درخت های جستجوی متوازن، نیازی ندارد که به صورت متناوب اقدام به برقراری توازن کند، اما به دلیل اینکه گره ها کاملاً پر نیستند، ممکن است مقداری حافظه هدر رود. حدود بالا و پایین شمارهٔ گره های فرزند، برای یک پیاده سازی خاص، به طور خاص تعیین شده اند. برای مثال در یک درخت بیِ ۳–۲ ( غالباً تنها با عنوان درخت ۳ - ۲ مورد اشاره قرار می گیرد ) ، هر گره ممکن است تنها ۲ یا ۳ گرهٔ فرزند داشته باشد.
یک درخت بی با استلزام اینکه همهٔ برگ ها در یک عمق قرار داشته باشند، به صورت متوازن نگه داشته می شود. این عمق از طریق عناصری که به درخت اضافه می شوند کم کم افزایش می یابد، ولی افزایش در عمق سراسری، کم اتفاق می افتد و وجود یک گرهٔ اضافیِ دورتر از ریشه را نتیجه می دهد.
درخت های بی، هنگامی که زمان دسترسی به گره ها به میزان قابل توجهی بیشتر از زمان پیمایش بین دو گره باشد، مزیت هایی اساسی بر دیگر انواع پیاده سازی دارند. این اتفاق معمولاً زمانی رخ می دهد که گره ها در حافظه ای ثانویه مانند دیسک سخت قرار دارند. به واسطهٔ بییشینه نمودن تعداد فرزندانِ هر گرهٔ درونی، ارتفاع درخت افزایش می یابد، توازن کم تر رخ می دهد، و کارایی بالا می رود. معمولاً این مقدار طوری تنظیم می شود که هر گره، یک بلاک کامل از دیسک یا مقداری برابر از حافظهٔ ثانویه را اشغال کند. هنگامی که درخت های بیِ ۳–۲ ممکن است در حافظهٔ اصلی مفید واقع شوند، اگر اندازهٔ گره ها به اندازهٔ یک بلاک دیسک تنظیم شوند، نتیجه ممکن است، یک درخت بیِ ۵۱۳–۲۵۷ باشد ( که در آن اندازه ها از توان های بزرگ تر ۲ هستند ) . یک درخت بی از مرتبهٔ m ( بیشینهٔ تعداد فرزندان هر گره ) درختی است که خصوصیات زیر را برآورده می کند: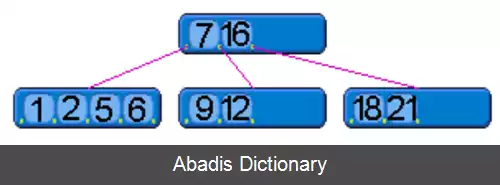
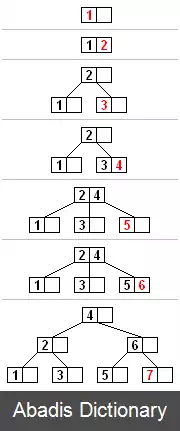
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر درخت بی، گره های درونی ( و نه برگ ها ) می توانند یک شمارهٔ متغیر از محدوده ای ازپیش تعریف شده مربوط به گره های فرزند را اختیار کنند. زمانی که داده ها درج شده یا از یک گره حذف می شوند، شمارهٔ گره های فرزند آن ها تغییر می کند. به منظور نگه داری محدودهٔ ازپیش تعریف شده، ممکن است گره های درونی به هم متصل شده یا از هم جدا شوند. به دلیل اینکه محدوده ای از گره های فرزند مجاز هستند، درخت بی، همانند دیگر درخت های جستجوی متوازن، نیازی ندارد که به صورت متناوب اقدام به برقراری توازن کند، اما به دلیل اینکه گره ها کاملاً پر نیستند، ممکن است مقداری حافظه هدر رود. حدود بالا و پایین شمارهٔ گره های فرزند، برای یک پیاده سازی خاص، به طور خاص تعیین شده اند. برای مثال در یک درخت بیِ ۳–۲ ( غالباً تنها با عنوان درخت ۳ - ۲ مورد اشاره قرار می گیرد ) ، هر گره ممکن است تنها ۲ یا ۳ گرهٔ فرزند داشته باشد.
یک درخت بی با استلزام اینکه همهٔ برگ ها در یک عمق قرار داشته باشند، به صورت متوازن نگه داشته می شود. این عمق از طریق عناصری که به درخت اضافه می شوند کم کم افزایش می یابد، ولی افزایش در عمق سراسری، کم اتفاق می افتد و وجود یک گرهٔ اضافیِ دورتر از ریشه را نتیجه می دهد.
درخت های بی، هنگامی که زمان دسترسی به گره ها به میزان قابل توجهی بیشتر از زمان پیمایش بین دو گره باشد، مزیت هایی اساسی بر دیگر انواع پیاده سازی دارند. این اتفاق معمولاً زمانی رخ می دهد که گره ها در حافظه ای ثانویه مانند دیسک سخت قرار دارند. به واسطهٔ بییشینه نمودن تعداد فرزندانِ هر گرهٔ درونی، ارتفاع درخت افزایش می یابد، توازن کم تر رخ می دهد، و کارایی بالا می رود. معمولاً این مقدار طوری تنظیم می شود که هر گره، یک بلاک کامل از دیسک یا مقداری برابر از حافظهٔ ثانویه را اشغال کند. هنگامی که درخت های بیِ ۳–۲ ممکن است در حافظهٔ اصلی مفید واقع شوند، اگر اندازهٔ گره ها به اندازهٔ یک بلاک دیسک تنظیم شوند، نتیجه ممکن است، یک درخت بیِ ۵۱۳–۲۵۷ باشد ( که در آن اندازه ها از توان های بزرگ تر ۲ هستند ) . یک درخت بی از مرتبهٔ m ( بیشینهٔ تعداد فرزندان هر گره ) درختی است که خصوصیات زیر را برآورده می کند:


wiki: درخت بی
