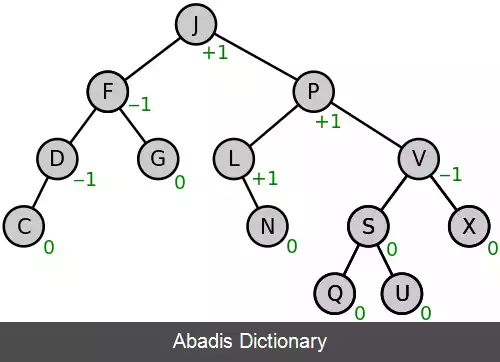
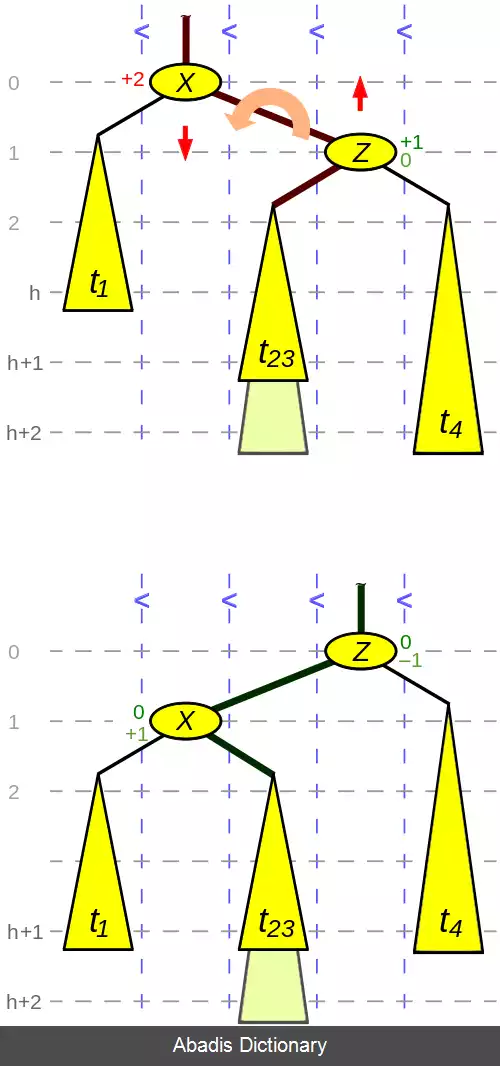
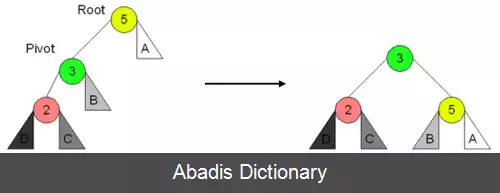
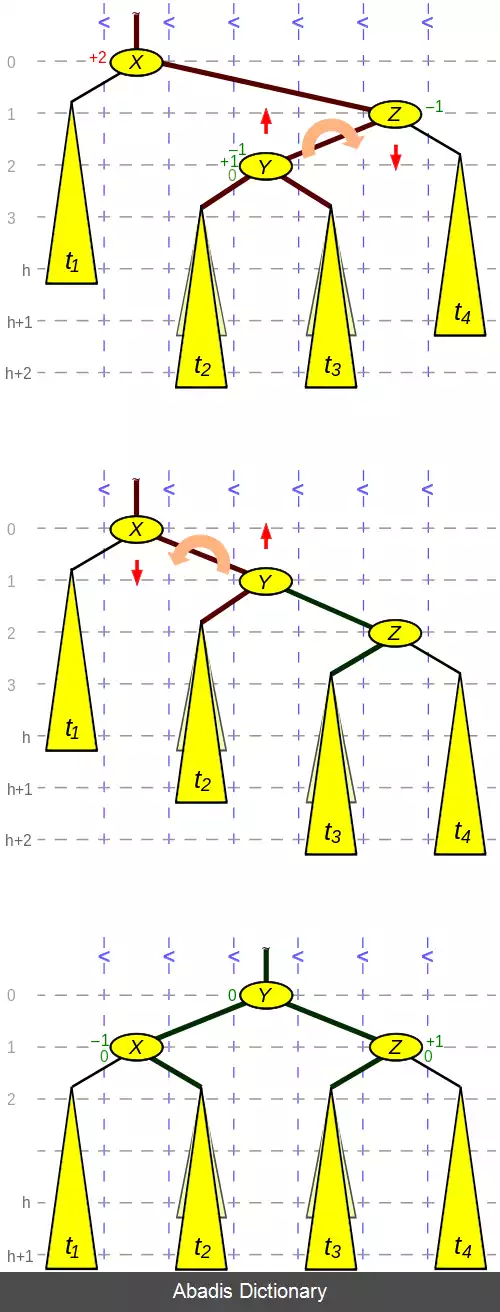
الگوریتم یا علوم رایانه، درخت ای وی ال ( به انگلیسی: AVL tree ) ، یک نوع درخت جستجوی دودویی خود متوازن کننده است و اولین ساختار داده ای از این نوع می باشد که اختراع شد. [ ۱] در یک درخت ای وی ال اختلاف ارتفاع دو زیر شاخهٔ هر گره حداکثر برابر یک است؛ بنابراین به این درخت، درخت با ارتفاع متوازن نیز گفته می شود. توجه کنید که عملیات درج، حذف و جستجو در یک درخت ای وی ال در بدترین حالت و حالت متوسط به اندازه O ( l g ( n ) ) خواهد بود به طوری که n تعداد گره های درخت می باشد. در عملیات درج و حذف ممکن است نیاز باشد که درخت به وسیله چرخش درخت ها، یک یا چند بار متوازن گردد.
عنوان AVL TREE از اول نام های دو مخترع آن به نام های G. M. Adelson - Velsky و E. M. Landis، که مقاله خود را در سال ۱۹۶۲ با موضوع «یک الگوریتم برای سازماندهی اطلاعات» منتشر کردند گرفته شده است.
درخت های ای وی ال غالباً با درخت های قرمز - سیاه مقایسه می شود. دلیل آن این است که هر دو داده ساختار قادر به انجام یک مجموعه از عملیات یکسان می باشند. در درخت های قرمز - سیاه نیز زمان لازم برای انجام عملیات اساسی به اندازه O ( l g ( n ) ) است. درخت های ای وی ال برای کاربردهای وسیع و گسترده جستجو بهتر از درخت های قرمز - سیاه هستند. الگوریتم های متوازن کردن درخت ها در بسیاری از دوره های علوم رایانه ظاهر شده و مورد استفاده قرار می گیرد. [ ۲]
ضریب توازن هر گره، تفاضل ارتفاع زیردرخت چپ آن گره از ارتفاع زیردرخت راست آن گره است. برای راس n داریم:
B a l a n c e F a c t o r := H e g h t ( R i g h t S u b t r e e ( n ) ) − H e g h t ( L e f t S u b t r e e ( n ) ) [ ۳]
هر گره ای که ضریب توازن آن برابر ۱، ۰ یا ۱ - باشد به عنوان گره متوازن در نظر گرفته می شود. هر درخت جست وجوی دودویی که تمام راس های آن متوازن باشند درخت ای وی ال است.
با دانستن تعریف یک درخت ای وی ال و ضریب توازن، با اضافه شدن گره جدید و تغییر ارتفاع، می توان یک درخت ای وی ال را متوازن نگه داشت. دقت شود که نیازی به نگه داشتن ارتفاع دقیق هر گره نیست. تنها کافی است برای هر گره ضریب توازن را نگه داریم. در روش قدیمی برای هر گره دو بیت نگه داشته می شد ولی تحقیقات بعدی نشان داد که تنها یک بیت برای هر گره کافی است. به این صورت که برای در هر گره تفاضل ارتفاع گره با از ارتفاع پدرش ذخیره می شود و همان طور که واضح است این مقدار همواره برابر ۱ یا ۲ است. ارتفاع هر درخت ای وی ال با تعداد n گره همواره در محدوده زیر قرار دارد:

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفعنوان AVL TREE از اول نام های دو مخترع آن به نام های G. M. Adelson - Velsky و E. M. Landis، که مقاله خود را در سال ۱۹۶۲ با موضوع «یک الگوریتم برای سازماندهی اطلاعات» منتشر کردند گرفته شده است.
درخت های ای وی ال غالباً با درخت های قرمز - سیاه مقایسه می شود. دلیل آن این است که هر دو داده ساختار قادر به انجام یک مجموعه از عملیات یکسان می باشند. در درخت های قرمز - سیاه نیز زمان لازم برای انجام عملیات اساسی به اندازه O ( l g ( n ) ) است. درخت های ای وی ال برای کاربردهای وسیع و گسترده جستجو بهتر از درخت های قرمز - سیاه هستند. الگوریتم های متوازن کردن درخت ها در بسیاری از دوره های علوم رایانه ظاهر شده و مورد استفاده قرار می گیرد. [ ۲]
ضریب توازن هر گره، تفاضل ارتفاع زیردرخت چپ آن گره از ارتفاع زیردرخت راست آن گره است. برای راس n داریم:
B a l a n c e F a c t o r := H e g h t ( R i g h t S u b t r e e ( n ) ) − H e g h t ( L e f t S u b t r e e ( n ) ) [ ۳]
هر گره ای که ضریب توازن آن برابر ۱، ۰ یا ۱ - باشد به عنوان گره متوازن در نظر گرفته می شود. هر درخت جست وجوی دودویی که تمام راس های آن متوازن باشند درخت ای وی ال است.
با دانستن تعریف یک درخت ای وی ال و ضریب توازن، با اضافه شدن گره جدید و تغییر ارتفاع، می توان یک درخت ای وی ال را متوازن نگه داشت. دقت شود که نیازی به نگه داشتن ارتفاع دقیق هر گره نیست. تنها کافی است برای هر گره ضریب توازن را نگه داریم. در روش قدیمی برای هر گره دو بیت نگه داشته می شد ولی تحقیقات بعدی نشان داد که تنها یک بیت برای هر گره کافی است. به این صورت که برای در هر گره تفاضل ارتفاع گره با از ارتفاع پدرش ذخیره می شود و همان طور که واضح است این مقدار همواره برابر ۱ یا ۲ است. ارتفاع هر درخت ای وی ال با تعداد n گره همواره در محدوده زیر قرار دارد:






wiki: درخت ای وی ال
