درخت آرایه درهم. در علوم رایانه درخت آرایه درهم داده ساختاری از نوع آرایه پویا می باشد که توسط ادوارد سیتارسکی در سال ۱۹۹۶ ارائه شد.
این نوع داده ساختار بر خلاف آرایه های پویای ساده که داده های خود را در یک قسمت از حافظه به صورت پشت سرهم نگه می دارند، از یک آرایه از حافظه های مجزا ( یا برگ ها ) برای نگهداری عناصر اطلاعات استفاده می کند. هدف اولیه این داده ساختار کاهش عملیات کپی کردن درایه ها به علت تغییر خودکار اندازهٔ آرایه و بهبود الگوهای استفاده از حافظه است.
در حالی که آرایه های پویای ساده که بر پایهٔ گسترش هندسی کار می کنند و از حافظهٔ خطی ( Ω ( n ) ) استفاده می کنند که n تعداد درایه های آرایه می باشد، درخت آرایه درهم فقط از حافظه ای از مرتبه ( n ) O استفاده می کند. بهینه سازی الگوریتم می تواند به طور کامل عملیات کپی کردن درایه ها را هنگام تغییر اندازهٔ آرایه حذف کند ولی با این کار فضای زیادی هدر خواهد شد.
در این نوع داده ساختار دسترسی به داده ها در زمان ثابت O ( 1 ) امکان پذیر است، اگرچه از آرایه های پویای معمولی کمی کندتر عمل می کند. در این الگوریتم هزینهٔ سرشکن درج یک سری از اشیا به انتهای درخت آرایه درهم از O ( 1 ) خواهد بود. برخلاف نامش این نوع داده ساختار از توابع درهم سازی استفاده نمی کند.
بنا به تعریف ادوارد سیتارسکی، درخت آرایه درهم یک لیست راهنمای سطح بالا دارد که شامل آرایه ای از برگ ها به تعداد توان دوم اندازه اش می باشد. تمامی آرایه های برگی، هم اندازه با لیست راهنمای سطح بالا می باشند. این ساختار از لحاظ ظاهری شباهت بسیاری به جدول درهم سازی با برخوردهای زنجیره ای بر اساس آرایه دارد که همین تشابه علت نام گذاری اش هم می باشد.
یک درخت آرایه درهم کامل می تواند m 2 درایه را در خود نگه دارد که m اندازهٔ لیست راهنمای سطح بالا می باشد. استفاده از توان دوم این قابلیت را می دهد که آدرس دهی فیزیکی از طریق عملیات بیتی به جای عملیات حسابی خارج قسمت و باقی مانده با سرعت بیشتری انجام شود و هم چنین تضمین می کند هزینهٔ سرشکن عملیات درج با وجود کپی کردن گاه و بیگاه سراسری به هنگام توسعه، هم چنان از O ( 1 ) خواهد بود.
در آرایه پویای معمولی که از رویهٔ گسترش هندسی استفاده می کند، وقتی آرایه پر می شود، یک قطعه از حافظه به اندازهٔ دو برابر اندازهٔ فعلی به صورت پشت سرهم گرفته می شود و کل داده ها به مکان جدید انتقال می یابند. این روش تضمین می کند که هنگامی که آرایهٔ توسعه یافته به نیمه ظرفیت جدیدش انتقال می یابد، هزینهٔ سر شکن عملیات از O ( 1 ) و هزینهٔ استفاده از حافظه از O ( n ) خواهد بود.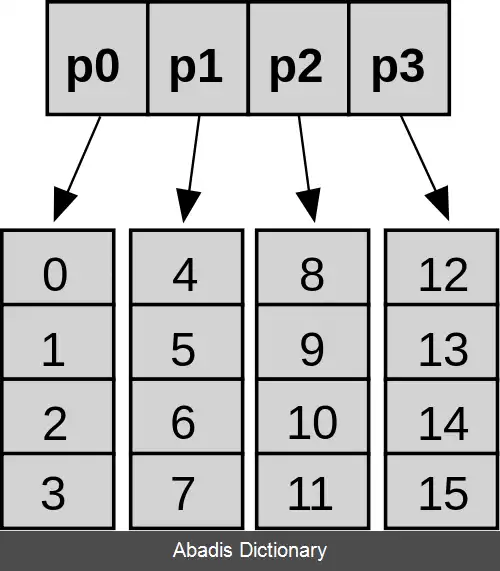
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین نوع داده ساختار بر خلاف آرایه های پویای ساده که داده های خود را در یک قسمت از حافظه به صورت پشت سرهم نگه می دارند، از یک آرایه از حافظه های مجزا ( یا برگ ها ) برای نگهداری عناصر اطلاعات استفاده می کند. هدف اولیه این داده ساختار کاهش عملیات کپی کردن درایه ها به علت تغییر خودکار اندازهٔ آرایه و بهبود الگوهای استفاده از حافظه است.
در حالی که آرایه های پویای ساده که بر پایهٔ گسترش هندسی کار می کنند و از حافظهٔ خطی ( Ω ( n ) ) استفاده می کنند که n تعداد درایه های آرایه می باشد، درخت آرایه درهم فقط از حافظه ای از مرتبه ( n ) O استفاده می کند. بهینه سازی الگوریتم می تواند به طور کامل عملیات کپی کردن درایه ها را هنگام تغییر اندازهٔ آرایه حذف کند ولی با این کار فضای زیادی هدر خواهد شد.
در این نوع داده ساختار دسترسی به داده ها در زمان ثابت O ( 1 ) امکان پذیر است، اگرچه از آرایه های پویای معمولی کمی کندتر عمل می کند. در این الگوریتم هزینهٔ سرشکن درج یک سری از اشیا به انتهای درخت آرایه درهم از O ( 1 ) خواهد بود. برخلاف نامش این نوع داده ساختار از توابع درهم سازی استفاده نمی کند.
بنا به تعریف ادوارد سیتارسکی، درخت آرایه درهم یک لیست راهنمای سطح بالا دارد که شامل آرایه ای از برگ ها به تعداد توان دوم اندازه اش می باشد. تمامی آرایه های برگی، هم اندازه با لیست راهنمای سطح بالا می باشند. این ساختار از لحاظ ظاهری شباهت بسیاری به جدول درهم سازی با برخوردهای زنجیره ای بر اساس آرایه دارد که همین تشابه علت نام گذاری اش هم می باشد.
یک درخت آرایه درهم کامل می تواند m 2 درایه را در خود نگه دارد که m اندازهٔ لیست راهنمای سطح بالا می باشد. استفاده از توان دوم این قابلیت را می دهد که آدرس دهی فیزیکی از طریق عملیات بیتی به جای عملیات حسابی خارج قسمت و باقی مانده با سرعت بیشتری انجام شود و هم چنین تضمین می کند هزینهٔ سرشکن عملیات درج با وجود کپی کردن گاه و بیگاه سراسری به هنگام توسعه، هم چنان از O ( 1 ) خواهد بود.
در آرایه پویای معمولی که از رویهٔ گسترش هندسی استفاده می کند، وقتی آرایه پر می شود، یک قطعه از حافظه به اندازهٔ دو برابر اندازهٔ فعلی به صورت پشت سرهم گرفته می شود و کل داده ها به مکان جدید انتقال می یابند. این روش تضمین می کند که هنگامی که آرایهٔ توسعه یافته به نیمه ظرفیت جدیدش انتقال می یابد، هزینهٔ سر شکن عملیات از O ( 1 ) و هزینهٔ استفاده از حافظه از O ( n ) خواهد بود.

wiki: درخت آرایه درهم
