در رایانش توزیع شده و نظریه گراف هندسی، برازش حریصانه، یک روند اختصاص دادن مختصات راس های یک شبکهٔ مخابراتی است که قابلیت مسیریابی جغرافیایی حریصانه برای مسیر دادن پیام ها در داخل شبکه را فراهم می کند. اگرچه برازش حریصانه برای استفاده در حسگر شبکه های بی سیم پیشنهاد شده است، که در آن راس ها در فضای فیزیکی مکان دهی شده اند، این مکان های موجود می توانند با مکان های داده شده توسط برازش حریصانه تفاوت داشته باشند، که در بعضی از موارد می تواند نقاطی از یک فضای مجازی ای از یک بعد بالاتر یا در یک هندسه نااقلیدسی باشند. از این دید، برازش حریصانه را می توان مانند یک روش کشیدن گراف در نظر گرفت، که در آن یک گراف انتزاعی ( شبکهٔ ارتباطات ) در یک فضای هندسی برازش می شود.
ایدهٔ انجام مسیریابی جغرافیایی با استفاده از مختصات در یک فضای مجازی، به جای استفاده از مختصات فیزیکی، به دلیل راو ات آل[ ۱] است. پیش رفت های بعدی نشان داده اند که تمام شبکه ها دارای برازش حریصانه با مختصات فشرده راس ها در هندسه هذلولوی هستند، که بعضی گراف ها، شامل گراف های چندضلعی، در فضای دوبعدی دارای برازش حریصانه اند، و این که گراف های حلقه - واحد، در فضاهای اقلیدسی بعدهای متوسط با عوامل کشش کم، دارای برازش حریصانه اند.
در مسیریابی حریصانه، یک پیام از یک راس مبدأ s به یک راس مقصد t، با یک سری قدم در بین راس های میانی سفر می کند، که هر کدام از آن قدم ها، پیام را به یک راس مجاور می دهد که به t نزدیک تر است. اگر پیام به یک راس میانی x برسد که راس مجاور نزدیک تری به t نداشته باشد، پس نمی توان پیش رفت کرد، و روند مسیریابی حریصانه شکست می خورد. یک برازش حریصانه، برازشی است از گراف داده شده، با ویژگی ای که این گونه شکست غیرممکن باشد. پس، می توان برازش حربصانه را برازشی از گراف تعریف کرد که برای هر دو راس x و t، یک راس مجاور x به نام y وجود دارد که y به t نزدیک تر است. [ ۲]
هر گرافی در فضای دوبعدی دارای برازش حریصانه نیست؛ یک مثال نقض ساده، ستارهٔ شش پر K1, 6 است، درختی با یک راس میانی و شش برگ. [ ۲] به طوری که در هر برازش این گراف، دو برگ وجود دارند که زاویهٔ بین آن ها، کمترمساوی ۶۰ درجه اند، که نتیجه می شود که حداقل یکی از این دو راس، راس مجاوری که به راس دیگر نزدیک تر باشد ندارند.
در فضاهای اقلیدسی با بعدهای بالا، گراف های بیش تری دارای برازش حریصانه اند؛ برای مثال، ستارهٔ شش پر در فضای سه بعدی دارای برازش حریصانه است، به طوری که راس میانی در مرکز و برگ ها هر کدام در فاصلهٔ واحد از مرکز در شش جهت بردار نشان هستند. البته، در هر فضا با بعد ثابت، گراف هایی هستند که نمی توانند حریصانه برازش شوند؛ زمانی که n, از عدد تماس یک فضا، بیش تر باشد، ستارهٔ nپر دارای برازش حریصانه نیست. [ ۳]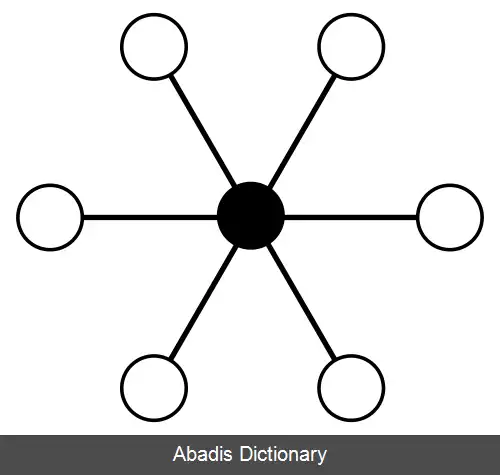
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفایدهٔ انجام مسیریابی جغرافیایی با استفاده از مختصات در یک فضای مجازی، به جای استفاده از مختصات فیزیکی، به دلیل راو ات آل[ ۱] است. پیش رفت های بعدی نشان داده اند که تمام شبکه ها دارای برازش حریصانه با مختصات فشرده راس ها در هندسه هذلولوی هستند، که بعضی گراف ها، شامل گراف های چندضلعی، در فضای دوبعدی دارای برازش حریصانه اند، و این که گراف های حلقه - واحد، در فضاهای اقلیدسی بعدهای متوسط با عوامل کشش کم، دارای برازش حریصانه اند.
در مسیریابی حریصانه، یک پیام از یک راس مبدأ s به یک راس مقصد t، با یک سری قدم در بین راس های میانی سفر می کند، که هر کدام از آن قدم ها، پیام را به یک راس مجاور می دهد که به t نزدیک تر است. اگر پیام به یک راس میانی x برسد که راس مجاور نزدیک تری به t نداشته باشد، پس نمی توان پیش رفت کرد، و روند مسیریابی حریصانه شکست می خورد. یک برازش حریصانه، برازشی است از گراف داده شده، با ویژگی ای که این گونه شکست غیرممکن باشد. پس، می توان برازش حربصانه را برازشی از گراف تعریف کرد که برای هر دو راس x و t، یک راس مجاور x به نام y وجود دارد که y به t نزدیک تر است. [ ۲]
هر گرافی در فضای دوبعدی دارای برازش حریصانه نیست؛ یک مثال نقض ساده، ستارهٔ شش پر K1, 6 است، درختی با یک راس میانی و شش برگ. [ ۲] به طوری که در هر برازش این گراف، دو برگ وجود دارند که زاویهٔ بین آن ها، کمترمساوی ۶۰ درجه اند، که نتیجه می شود که حداقل یکی از این دو راس، راس مجاوری که به راس دیگر نزدیک تر باشد ندارند.
در فضاهای اقلیدسی با بعدهای بالا، گراف های بیش تری دارای برازش حریصانه اند؛ برای مثال، ستارهٔ شش پر در فضای سه بعدی دارای برازش حریصانه است، به طوری که راس میانی در مرکز و برگ ها هر کدام در فاصلهٔ واحد از مرکز در شش جهت بردار نشان هستند. البته، در هر فضا با بعد ثابت، گراف هایی هستند که نمی توانند حریصانه برازش شوند؛ زمانی که n, از عدد تماس یک فضا، بیش تر باشد، ستارهٔ nپر دارای برازش حریصانه نیست. [ ۳]

wiki: درج کردن حریصانه
