در علم ریاضیات دامنه ی ( به انگلیسی: Domain ) یک تابع عبارت است از مجموع مقادیر مجاز ورودی به یک تابع که منجر به تولید خروجی ( برد ) می شود. [ ۱] به بیان دیگر مؤلفه های اول هر تابع که به صورت زوج مرتب نوشته شده باشد را دامنه می گویند و به صورت Df نوشته می شود .
یعنی تابع مورد نظر در چه بازه ای تعریف شده است. با توجه به انواع توابع ابتدا باید نوع تابع را بشناسیم.
تعبیر هندسی:
اگر نمودار تابع را داشته باشیم تصویر نمودار بر روی محور xها همان دامنه تعریف تابع است.
دامنه این توابع R ( مجموعه اعداد حقیقی ) است. مگر اینکه خود ضابطه، دامنه را محدود کرده باشد.
در زوج مرتب ها مولفه های اول، دامنه می باشد.
مثال زیر را ببینید:
A = { ( 4 , 8 ) , ( 9 , 7 ) , ( 12 , 46 ) , ( 78 , 52 ) }
در این تابع دامنه برابر است با:
D A = { 4 , 9 , 12 , 78 }
اگر نمودار تابع را داشته باشیم تصویر نمودار بر روی محور xها همان دامنه ی تعریف تابع است.
برای تشخیص دامنه از روی نمودار، ابتدا و انتها نمودار را به محور x ها وصل می کنیم. در نهایت بازه مشخص شده برابر با همان دامنه است.
نکته: حواستان به باز و بسته بودن ابتدا و انتها نمودار باشد.
نکته: ممکن است نمودار چندضابطه ای باشد. مثلا در محدوده ای نمودار تعریف نشده باشد. آن وقت حواسمان باید به آن ناحیه ها باشد و آنجا را جز دامنه حساب نکنیم.
نکته: حواستان به توپر یا توخالی بودن آخر و ابتدا نمودار باشد. زیرا:
• اگر توخالی باشد بازه ی دامنه باز است.
• اگر توپر باشد بازه ی دامنه بسته است.
تابعی به شکل زیر:
P ( x ) Q ( x ) دامنه این توابع اعداد حقیقی بجز ریشه های مخرج است. یعنی اعدادی که مقدار مخرج را صفر می کند.
باید زیر رادیکال نامنفی ( بزرگتر و مساوی صفر - 0 ≥ عبارت زیر رادیکال ) باشد.
نکته دامنه توابع رادیکالی با فرجه فرد همانند توابع چندجمله ای است.
دامنه و برد تابع «سیده فاطمه موسوی نطنزی»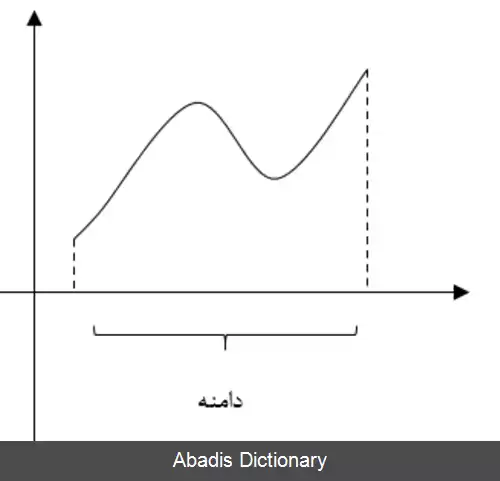
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیعنی تابع مورد نظر در چه بازه ای تعریف شده است. با توجه به انواع توابع ابتدا باید نوع تابع را بشناسیم.
تعبیر هندسی:
اگر نمودار تابع را داشته باشیم تصویر نمودار بر روی محور xها همان دامنه تعریف تابع است.
دامنه این توابع R ( مجموعه اعداد حقیقی ) است. مگر اینکه خود ضابطه، دامنه را محدود کرده باشد.
در زوج مرتب ها مولفه های اول، دامنه می باشد.
مثال زیر را ببینید:
A = { ( 4 , 8 ) , ( 9 , 7 ) , ( 12 , 46 ) , ( 78 , 52 ) }
در این تابع دامنه برابر است با:
D A = { 4 , 9 , 12 , 78 }
اگر نمودار تابع را داشته باشیم تصویر نمودار بر روی محور xها همان دامنه ی تعریف تابع است.
برای تشخیص دامنه از روی نمودار، ابتدا و انتها نمودار را به محور x ها وصل می کنیم. در نهایت بازه مشخص شده برابر با همان دامنه است.
نکته: حواستان به باز و بسته بودن ابتدا و انتها نمودار باشد.
نکته: ممکن است نمودار چندضابطه ای باشد. مثلا در محدوده ای نمودار تعریف نشده باشد. آن وقت حواسمان باید به آن ناحیه ها باشد و آنجا را جز دامنه حساب نکنیم.
نکته: حواستان به توپر یا توخالی بودن آخر و ابتدا نمودار باشد. زیرا:
• اگر توخالی باشد بازه ی دامنه باز است.
• اگر توپر باشد بازه ی دامنه بسته است.
تابعی به شکل زیر:
P ( x ) Q ( x ) دامنه این توابع اعداد حقیقی بجز ریشه های مخرج است. یعنی اعدادی که مقدار مخرج را صفر می کند.
باید زیر رادیکال نامنفی ( بزرگتر و مساوی صفر - 0 ≥ عبارت زیر رادیکال ) باشد.
نکته دامنه توابع رادیکالی با فرجه فرد همانند توابع چندجمله ای است.
دامنه و برد تابع «سیده فاطمه موسوی نطنزی»

wiki: دامنه تابع
