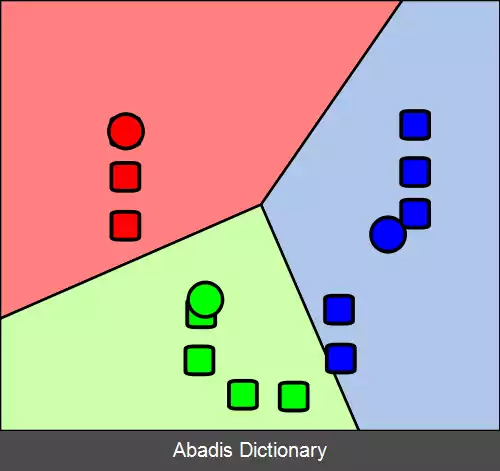
خوشه بندی کی - میانگین ( به انگلیسی: k - means clustering ) روشی در کمی سازی بردارهاست که در اصل از پردازش سیگنال گرفته شده و برای آنالیز خوشه بندی در داده کاوی محبوب است. کی - میانگین خوشه بندی با هدف تجزیه n مشاهدات به k خوشه است که در آن هر یک از مشاهدات متعلق به خوشهای با نزدیکترین میانگین آن است، این میانگین به عنوان پیش نمونه استفاده می شود. این به پارتیشن بندی داده های به یک دیاگرام ورونوی تبدیل می شود.
اصطلاح کی - میانگین ( به انگلیسی: K - Means Clustering ) برای اولین بار توسط جیمز بی مک کوین ( استاد دانشگاه کالیفرنیا ) در سال ۱۹۶۷ مورد استفاده قرار گرفت، [ ۱] هرچند این ایده به هوگو استین هاوس در سال ۱۹۵۷ باز می گردد. [ ۲] این الگوریتم ابتدا توسط استوارت لویید در سال ۱۹۵۷ به عنوان یک تکنیک برای مدولاسیون کد پالس پیشنهاد شد و تا سال ۱۹۸۲ خارج از آزمایشگاه های بل به انتشار نرسید. [ ۳] فورجی در سال ۱۹۶۵ الگوریتمی مشابه را منتشر کرد، به همین دلیل این الگوریتم، الگوریتم لویید - فورجی نیز نامیده می شود. [ ۴]
با توجه به مجموعه ای از مشاهدات ( x 1 , x 2 , ⋯ , x n ) که در آن هر یک از مشاهدات یک بردار حقیقی d - بعدی است. خوشه بندی کی - میانگین با هدف پارتیشن بندی n مشاهدات به k ≤ n مجموعه S = { S 1 , S 2 , ⋯ , S k } است به طوری که مجموع مربع اختلاف از میانگین ( یعنی واریانس ) برای هر خوشه حداقل شود. تعریف دقیق ریاضی آن به این شکل است:
که در آن μ i میانگین نقاط در S i است. این معادل است با به حداقل رساندن دو به دو مربع انحراف از نقاط در همان خوشه:
چون کل واریانس ثابت است، از قانون واریانس کلی می توان نتیجه گرفت که این معادله برابر است با بیشینه کردن مربع انحرافات بین نقاط خوشه های مختلف ( BCSS ) . [ ۵]
رایج ترین الگوریتم کی - میانگین با استفاده از یک تکرار شونده پالایش کار می کند. این الگوریتم به طور معمول با نام الگوریتم کی - میانگین شناخته می شود، اما در میان جامعه علوم کامپیوتر، اغلب آن را با عنوان الگوریتم لوید می شناسند.
الگوریتم به این شکل عمل می کند:[ ۶]
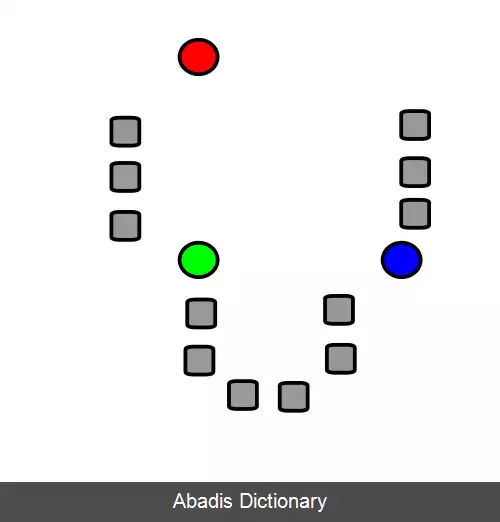
• ابتدا k {\displaystyle k} میانگین یعنی ( μ 1 ( 0 ) , μ 2 ( 0 ) , ⋯ , μ k ( 0 ) ) {\displaystyle \left ( \mu _{1}^{ ( 0 ) }, \mu _{2}^{ ( 0 ) }, \cdots , \mu _{k}^{ ( 0 ) }\right ) } را که نماینده خوشه ها هستند، به صورت تصادفی مقداردهی می کنیم.
• سپس، این دو مرحله پایین را به تناوب چندین بار اجرا می کنیم تا میانگین ها به یک ثبات کافی برسند و یا مجموع واریانس های خوشه ها تغییر چندانی نکنند:
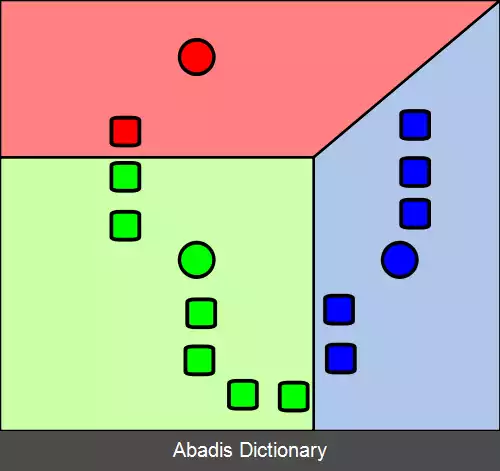
• از میانگین ها k {\displaystyle k} خوشه می سازیم، خوشه i {\displaystyle i} ام در زمان t {\displaystyle t} تمام داده هایی هستند که از لحاظ اقلیدسی کمترین فاصله را با میانگین μ i ( t ) {\displaystyle \mu _{i}^{ ( t ) }} یعنی میانگین i {\displaystyle i} ام در زمان t {\displaystyle t} دارند[ ۷] . به زبان ریاضی خوشه i {\displaystyle i} ام در زمان t {\displaystyle t} برابر خواهد بود با:
• S i ( t ) = { x p : ‖ x p − μ i ( t ) ‖ 2 ≤ ‖ x p − μ j ( t ) ‖ 2 ∀ j , 1 ≤ j ≤ k } {\displaystyle S_{i}^{ ( t ) }={\big \{}x_{p}:{\big \|}x_{p} - \mu _{i}^{ ( t ) }{\big \|}^{2}\leq {\big \|}x_{p} - \mu _{j}^{ ( t ) }{\big \|}^{2}\ \forall j, 1\leq j\leq k{\big \}}}
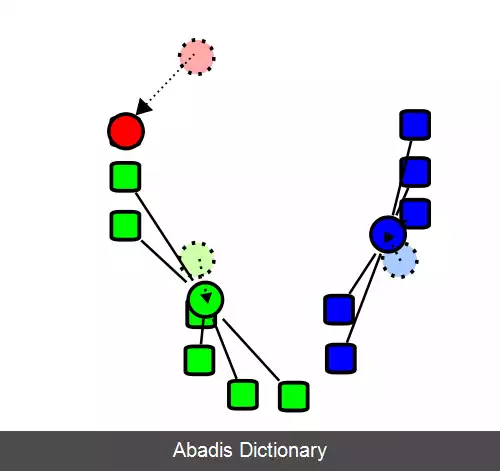
• حال میانگین ها را بر اساس این خوشه های جدید به این شکل بروز می کنیم:[ ۸]
• μ i ( t + 1 ) = 1 | S i ( t ) | ∑ x j ∈ S i ( t ) x j {\displaystyle \mu _{i}^{ ( t+1 ) }={\frac {1}{|S_{i}^{ ( t ) }|}}\sum _{x_{j}\in S_{i}^{ ( t ) }}x_{j}}
• در نهایت میانگین های مرحله آخر ( در زمان T {\displaystyle T} ) یعنی ( μ 1 ( T ) , μ 2 ( T ) , ⋯ , μ k ( T ) ) {\displaystyle \left ( \mu _{1}^{ ( T ) }, \mu _{2}^{ ( T ) }, \cdots , \mu _{k}^{ ( T ) }\right ) } خوشه ها را نمایندگی خواهند کرد.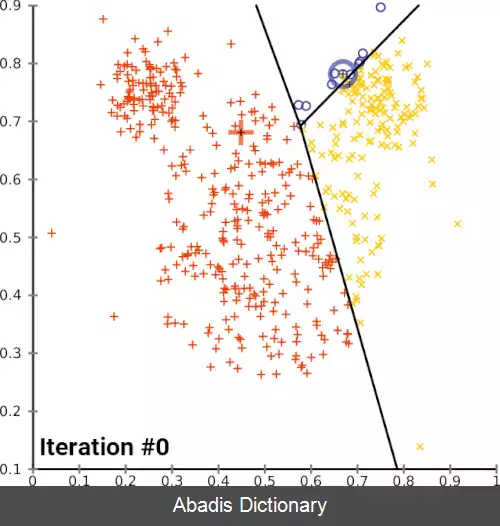
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاصطلاح کی - میانگین ( به انگلیسی: K - Means Clustering ) برای اولین بار توسط جیمز بی مک کوین ( استاد دانشگاه کالیفرنیا ) در سال ۱۹۶۷ مورد استفاده قرار گرفت، [ ۱] هرچند این ایده به هوگو استین هاوس در سال ۱۹۵۷ باز می گردد. [ ۲] این الگوریتم ابتدا توسط استوارت لویید در سال ۱۹۵۷ به عنوان یک تکنیک برای مدولاسیون کد پالس پیشنهاد شد و تا سال ۱۹۸۲ خارج از آزمایشگاه های بل به انتشار نرسید. [ ۳] فورجی در سال ۱۹۶۵ الگوریتمی مشابه را منتشر کرد، به همین دلیل این الگوریتم، الگوریتم لویید - فورجی نیز نامیده می شود. [ ۴]
با توجه به مجموعه ای از مشاهدات ( x 1 , x 2 , ⋯ , x n ) که در آن هر یک از مشاهدات یک بردار حقیقی d - بعدی است. خوشه بندی کی - میانگین با هدف پارتیشن بندی n مشاهدات به k ≤ n مجموعه S = { S 1 , S 2 , ⋯ , S k } است به طوری که مجموع مربع اختلاف از میانگین ( یعنی واریانس ) برای هر خوشه حداقل شود. تعریف دقیق ریاضی آن به این شکل است:
که در آن μ i میانگین نقاط در S i است. این معادل است با به حداقل رساندن دو به دو مربع انحراف از نقاط در همان خوشه:
چون کل واریانس ثابت است، از قانون واریانس کلی می توان نتیجه گرفت که این معادله برابر است با بیشینه کردن مربع انحرافات بین نقاط خوشه های مختلف ( BCSS ) . [ ۵]
رایج ترین الگوریتم کی - میانگین با استفاده از یک تکرار شونده پالایش کار می کند. این الگوریتم به طور معمول با نام الگوریتم کی - میانگین شناخته می شود، اما در میان جامعه علوم کامپیوتر، اغلب آن را با عنوان الگوریتم لوید می شناسند.
الگوریتم به این شکل عمل می کند:[ ۶]
• ابتدا k {\displaystyle k} میانگین یعنی ( μ 1 ( 0 ) , μ 2 ( 0 ) , ⋯ , μ k ( 0 ) ) {\displaystyle \left ( \mu _{1}^{ ( 0 ) }, \mu _{2}^{ ( 0 ) }, \cdots , \mu _{k}^{ ( 0 ) }\right ) } را که نماینده خوشه ها هستند، به صورت تصادفی مقداردهی می کنیم.
• سپس، این دو مرحله پایین را به تناوب چندین بار اجرا می کنیم تا میانگین ها به یک ثبات کافی برسند و یا مجموع واریانس های خوشه ها تغییر چندانی نکنند:
• از میانگین ها k {\displaystyle k} خوشه می سازیم، خوشه i {\displaystyle i} ام در زمان t {\displaystyle t} تمام داده هایی هستند که از لحاظ اقلیدسی کمترین فاصله را با میانگین μ i ( t ) {\displaystyle \mu _{i}^{ ( t ) }} یعنی میانگین i {\displaystyle i} ام در زمان t {\displaystyle t} دارند[ ۷] . به زبان ریاضی خوشه i {\displaystyle i} ام در زمان t {\displaystyle t} برابر خواهد بود با:
• S i ( t ) = { x p : ‖ x p − μ i ( t ) ‖ 2 ≤ ‖ x p − μ j ( t ) ‖ 2 ∀ j , 1 ≤ j ≤ k } {\displaystyle S_{i}^{ ( t ) }={\big \{}x_{p}:{\big \|}x_{p} - \mu _{i}^{ ( t ) }{\big \|}^{2}\leq {\big \|}x_{p} - \mu _{j}^{ ( t ) }{\big \|}^{2}\ \forall j, 1\leq j\leq k{\big \}}}
• حال میانگین ها را بر اساس این خوشه های جدید به این شکل بروز می کنیم:[ ۸]
• μ i ( t + 1 ) = 1 | S i ( t ) | ∑ x j ∈ S i ( t ) x j {\displaystyle \mu _{i}^{ ( t+1 ) }={\frac {1}{|S_{i}^{ ( t ) }|}}\sum _{x_{j}\in S_{i}^{ ( t ) }}x_{j}}
• در نهایت میانگین های مرحله آخر ( در زمان T {\displaystyle T} ) یعنی ( μ 1 ( T ) , μ 2 ( T ) , ⋯ , μ k ( T ) ) {\displaystyle \left ( \mu _{1}^{ ( T ) }, \mu _{2}^{ ( T ) }, \cdots , \mu _{k}^{ ( T ) }\right ) } خوشه ها را نمایندگی خواهند کرد.






wiki: خوشه بندی کی میانگین
