خطسانی یا خطینگی یا خطی بودن ( به انگلیسی: Linearity ) ، ویژگی یک رابطه یا عملکرد ریاضی است؛ به این معنی که می توان آن رابطه را در شکل نموداری به صورت یک خط مستقیم نشان داد. مثال های رابطهٔ خطی ولتاژ و جریان در یک مقاومت ( قانون اهم ) ، یا جِرم و وزن یک شیء است. تناسب بیانگر خطسانی است، اما خطی بودن لزوماً به معنای تناسب رابطه نیست.
در ریاضیات، یک نگاشت خطی یا تابع خطی f ( x ) تابعی است که دو ویژگی زیر را برآورده می کند:[ ۱]
• جمع پذیری ( Additive map ) : تابعی که عمل جمع را حفظ می کند: f ( x + y ) = f ( x ) + f ( y ) .
• همگن ( function Homogeneity ) درجهٔ ۱: f ( αx ) = αf ( x ) برای تمام α.
مفهوم رابطهٔ خطی را می توان به عملگرهای خطی گسترش داد. مثال های مهم از عملگرهای خطی مشتق را شامل می شود که عملگر دیفرانسیلی در نظر گرفته شده، و بسیاری از آن، از جمله عملگرهای دل و لاپلاس ساخته شده اند. هنگامی که یک معادله دیفرانسیلی را بتوان در شکل خطی بیان کرد، به طور کلی معادله به سادگی با شکستن آن به قطعات کوچک، و حل این قطعات، و در نهایت جمع کردن نتیجه ها، قابل حل است.
جبر خطی شاخه ای از ریاضیات است و به مطالعهٔ بردارها، فضاهای برداری ( همچنین فضاهای خطی نامیده می شود ) ، تحولات خطی ( همچنین به نام نگاشت خطی خوانده می شود ) و سیستم های معادلات خطی می پردازد.
واژهٔ خطی و واژهٔ لاتین آن ( لینیر linear ) به معنی «مربوط به خط» اشاره به مشابه خط بودن است، برای شرح معادلات خطی و غیر خطی، به مقاله های اصلی آنها مراجعه کنید. فیزیک دانان و ریاضیدانان به استفاده از معادلات و توابع غیر خطی علاقه مند هستند زیرا آن ها می توانند برای نشان دادن بسیاری از پدیده های طبیعی، از جمله آشوب، آن ها را به راحتی مورد استفاده قرار دهند.
در یک استفادهٔ متفاوت از تعریف فوق، به یک چندجمله ای درجهٔ ۱، خطی گفته می شود زیرا گراف یک تابع از آن به شکل یک خط است. [ ۲]
در حقیقت، یک معادلهٔ خطی یکی از اشکال:
توجه شود که این استفاده از اصطلاح خطی همانند بخش فوق نیست، زیرا چندجمله ای های خطی بر روی اعداد حقیقی، به طور کلی هیچ جمع بندی یا یکنواختی را برآورده نمی کنند. در حقیقت، اگر و فقط اگر «صفر = b» باشد، این کار را انجام می دهند؛ بنابراین در حالت «b ≠ ۰»، تابع اغلب یک تابع آفین نامیده می شود، ( تبدیل آفین را ببینید ) .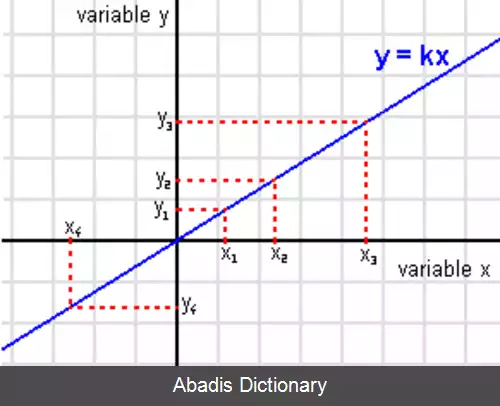
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر ریاضیات، یک نگاشت خطی یا تابع خطی f ( x ) تابعی است که دو ویژگی زیر را برآورده می کند:[ ۱]
• جمع پذیری ( Additive map ) : تابعی که عمل جمع را حفظ می کند: f ( x + y ) = f ( x ) + f ( y ) .
• همگن ( function Homogeneity ) درجهٔ ۱: f ( αx ) = αf ( x ) برای تمام α.
مفهوم رابطهٔ خطی را می توان به عملگرهای خطی گسترش داد. مثال های مهم از عملگرهای خطی مشتق را شامل می شود که عملگر دیفرانسیلی در نظر گرفته شده، و بسیاری از آن، از جمله عملگرهای دل و لاپلاس ساخته شده اند. هنگامی که یک معادله دیفرانسیلی را بتوان در شکل خطی بیان کرد، به طور کلی معادله به سادگی با شکستن آن به قطعات کوچک، و حل این قطعات، و در نهایت جمع کردن نتیجه ها، قابل حل است.
جبر خطی شاخه ای از ریاضیات است و به مطالعهٔ بردارها، فضاهای برداری ( همچنین فضاهای خطی نامیده می شود ) ، تحولات خطی ( همچنین به نام نگاشت خطی خوانده می شود ) و سیستم های معادلات خطی می پردازد.
واژهٔ خطی و واژهٔ لاتین آن ( لینیر linear ) به معنی «مربوط به خط» اشاره به مشابه خط بودن است، برای شرح معادلات خطی و غیر خطی، به مقاله های اصلی آنها مراجعه کنید. فیزیک دانان و ریاضیدانان به استفاده از معادلات و توابع غیر خطی علاقه مند هستند زیرا آن ها می توانند برای نشان دادن بسیاری از پدیده های طبیعی، از جمله آشوب، آن ها را به راحتی مورد استفاده قرار دهند.
در یک استفادهٔ متفاوت از تعریف فوق، به یک چندجمله ای درجهٔ ۱، خطی گفته می شود زیرا گراف یک تابع از آن به شکل یک خط است. [ ۲]
در حقیقت، یک معادلهٔ خطی یکی از اشکال:
توجه شود که این استفاده از اصطلاح خطی همانند بخش فوق نیست، زیرا چندجمله ای های خطی بر روی اعداد حقیقی، به طور کلی هیچ جمع بندی یا یکنواختی را برآورده نمی کنند. در حقیقت، اگر و فقط اگر «صفر = b» باشد، این کار را انجام می دهند؛ بنابراین در حالت «b ≠ ۰»، تابع اغلب یک تابع آفین نامیده می شود، ( تبدیل آفین را ببینید ) .

wiki: خطسانی
