حساب لامبدا ( به انگلیسی: Lambda Calculus ) ( که به حساب لاندا یا حساب λ یا λ - c a l c u l u s نیز معروف است ) ، دستگاه صوری در منطق ریاضی جهت بیان محاسبات براساس تجرید تابع و به کار بردن آن با استفاده از انقیاد نام و جایگیزینی است. این دستگاه، مدلی محاسباتی است که می توان از آن جهت شبیه سازی هر نوع ماشین تورینگی استفاده کرد. این دستگاه صوری، توسط آلونزو چرچ در دهه ۱۹۳۰ میلادی، به عنوان بخشی از تحقیقات او بر روی بنیان های ریاضیات معرفی گشت.
حساب لامبدا، شامل ساخت ترم های لامبدا و اعمال عملیات کاهشی ( تقلیلی ) رویشان است. در ساده ترین فرم حساب لامبدا، ترم ها تنها با استفاده از قواعد زیر ساخته می شوند:
با کمک این قواعد، عباراتی بدین شکل ساخته می گردند: ( λ x . λ y . ( λ z . ( λ x . z x ) ( λ y . z y ) ) ( x y ) ) . در صورتی که ابهامی ایجاد نشود، می توان پرانتزها را برداشت. در برخی از کاربردها، ترم های مربوط به ثوابت ریاضیاتی و منطقی، و همچنین عملگرها را نیز می توان در چنین عباراتی به کار برد.
عملیات کاهنده ( تقلیل دهنده ) شامل این موارد اند:
اگر از اندیس گذاری دو برویجن استفاده شود، آنگاه دیگر به تبدیل α نیازی نیست، چرا ه تصادم نام دیگر رخ نخواهد داد. اگر به کار بردن مکرر مراحل تقلیل در نهایت به پایان برسد، آنگاه با کمک قضیه چرچ - روسر، فرم نرمال β یی را تولید خواهد نمود.
اگر از تابع لامبدای جهانی استفاده شود، به نام متغیرهایی چون یوتا و جوت ( Iota and Jot ) ، که قادرند در ترکیبات مختلف، با صدا زدنشان بر روی خودشان، هر نوع رفتار تابع را ایجاد نمایند، دیگر نیاز نخواهد بود.
حساب لاندا یک تورینگ کامل است، به عبارت دیگر، یک مدل محاسبه عمومی ست که می تواند هر ماشین تورینگ یک نواره را شبیه سازی کند. [ ۱] حرف یونانی لاندا ( λ ) ، که در اسم این حساب حضور دارد، در عبارات لاندا و جملات لاندا برای نشان دادن انقیاد یک متغیر در یک تابع استفاده می شود.
حساب لاندا می تواند نوع دار ( Typed ) یا بدون نوع ( Untyped ) باشد. در حساب لاندای نوع دار یک تابع درصورتی می تواند صدا زده شود که توانایی پذیرش داده هایی با آن «نوع» خاص را داشته باشد. جبرهای لاندا نوع دار از لحاظ محاسباتی توانایی بیان کردن کمتری از جبرهای لاندای بدون نوع دارند؛ لذا از این جهت ضعیف تر هستند. اما از سوی دیگر قابلیت اثبات بالاتری دارند و می توانند چیزهای بیشتری را اثبات کنند. برای مثال در حساب لاندای نوع دار ساده، تمامی استراتژی های محاسبه تمام شدنی ( terminating ) هستند؛ در حالی که در حساب بدون نوع نیازی به تمام شدنی بودن نیست و محاسبه یک عبارت می تواند تا بینهایت ادامه پیدا کند.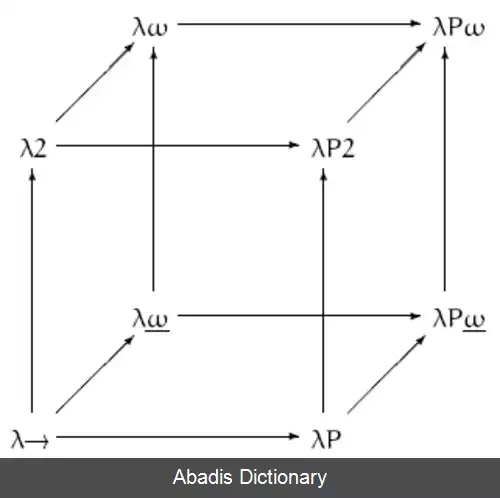
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفحساب لامبدا، شامل ساخت ترم های لامبدا و اعمال عملیات کاهشی ( تقلیلی ) رویشان است. در ساده ترین فرم حساب لامبدا، ترم ها تنها با استفاده از قواعد زیر ساخته می شوند:
با کمک این قواعد، عباراتی بدین شکل ساخته می گردند: ( λ x . λ y . ( λ z . ( λ x . z x ) ( λ y . z y ) ) ( x y ) ) . در صورتی که ابهامی ایجاد نشود، می توان پرانتزها را برداشت. در برخی از کاربردها، ترم های مربوط به ثوابت ریاضیاتی و منطقی، و همچنین عملگرها را نیز می توان در چنین عباراتی به کار برد.
عملیات کاهنده ( تقلیل دهنده ) شامل این موارد اند:
اگر از اندیس گذاری دو برویجن استفاده شود، آنگاه دیگر به تبدیل α نیازی نیست، چرا ه تصادم نام دیگر رخ نخواهد داد. اگر به کار بردن مکرر مراحل تقلیل در نهایت به پایان برسد، آنگاه با کمک قضیه چرچ - روسر، فرم نرمال β یی را تولید خواهد نمود.
اگر از تابع لامبدای جهانی استفاده شود، به نام متغیرهایی چون یوتا و جوت ( Iota and Jot ) ، که قادرند در ترکیبات مختلف، با صدا زدنشان بر روی خودشان، هر نوع رفتار تابع را ایجاد نمایند، دیگر نیاز نخواهد بود.
حساب لاندا یک تورینگ کامل است، به عبارت دیگر، یک مدل محاسبه عمومی ست که می تواند هر ماشین تورینگ یک نواره را شبیه سازی کند. [ ۱] حرف یونانی لاندا ( λ ) ، که در اسم این حساب حضور دارد، در عبارات لاندا و جملات لاندا برای نشان دادن انقیاد یک متغیر در یک تابع استفاده می شود.
حساب لاندا می تواند نوع دار ( Typed ) یا بدون نوع ( Untyped ) باشد. در حساب لاندای نوع دار یک تابع درصورتی می تواند صدا زده شود که توانایی پذیرش داده هایی با آن «نوع» خاص را داشته باشد. جبرهای لاندا نوع دار از لحاظ محاسباتی توانایی بیان کردن کمتری از جبرهای لاندای بدون نوع دارند؛ لذا از این جهت ضعیف تر هستند. اما از سوی دیگر قابلیت اثبات بالاتری دارند و می توانند چیزهای بیشتری را اثبات کنند. برای مثال در حساب لاندای نوع دار ساده، تمامی استراتژی های محاسبه تمام شدنی ( terminating ) هستند؛ در حالی که در حساب بدون نوع نیازی به تمام شدنی بودن نیست و محاسبه یک عبارت می تواند تا بینهایت ادامه پیدا کند.

wiki: حساب لامبدا
