حدس بازسازی برای اولین بار در سال ۱۹۴۲ مطرح شد. حدس بازسازی ادعا می کند هر گراف با استفاده از کارت های خود ( زیرگراف های رأس حذفی ) ، قابل بازسازی است. اگرچه تلاش های زیادی پیرامون این حدس صورت گرفته، اما مسئله در حالت کلی باز مانده است.
در این بخش ما مقدمه و تاریخچه ای مختصر از حدس بازسازی گراف را از سال ۱۹۴۱ بیان می کنیم. حدس بازسازی ادعا می کند که هر گراف ساده با حداقل ۳ رأس از روی زیرگراف های رأس حذفی آن با تقریب یکریختی قابل بازسازی است. [ ۱]
حدس بازسازی یکی از مشهورترین مسایل نظریهٔ گراف است، که همواره ذهن بسیاری از ریاضی دانان را به خود مشغول کرده است. هراری[ ۲] از این مسئله به خاطر ماهیت مسری آن به عنوان بیماری گرافی یاد می کرد. بر اساس گزارش های ثبت شده، ویسکُنسین در ۱۹۴۱، کِلی و اُلام به عنوان اولین قربانیان این بیماری شناخته می شوند. نمادها با توجه به نمادگذاری کتابِ باندی و مورتی[ ۳] انتخاب شده است؛ بنابراین گراف G دارای مجموعه رأس های V ( G ) , مجموعه یال های E ( G ) ؛ همچنین دارای v ( G ) رأس و ε ( G ) یال است. زیرگراف G v زیرگراف حاصل از حذف رأسِ v به همراهِ تمام یال های متصل به آن است. شکل ( ۱ ) زیرگراف های رأس حذفی گراف G را نشان می دهد.
برای فرمول بندی دقیق حدس نیاز به دو مفهوم زیر داریم:
یک بازسازی از گراف G ، یک گراف H است، به طوری که V ( G ) = V ( H ) و برای هر v ∈ V ( G ) ، داشته باشیم H v ≅ G v . همچنین می گوییم G قابل بازسازی است، اگر هر بازسازی از G با خود G یکریخت باشد.
به عنوان مثال K 2 و 2 K 1 بازسازی یکدیگرند. حدس بازسازی ادعا می کند این دو، تنها گراف های غیرقابل بازسازی هستند.
• حدس بازسازی:[ ۴] [ ۵] تمام گراف های متناهی، ساده و غیرجهت دار با حداقل سه رأس قابل بازسازی هستند.
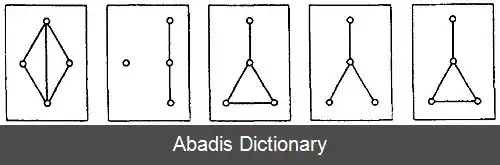
نگاه به مسئله به عنوان کارت هایی که هر زیرگراف روی آن ها رسم شده، خالی از لطف نیست. به طور نمونه گراف G در شکل ( ۲ ) دارای دسته کارتی مانند شکل ( ۵ ) است ( ارائه، توسط هَراری[ ۶] ) . نمایش مسئله با کارت ها، به طوری که گراف هایی که کارت ها را تولید می کنند بیابیم بسیار مرسوم است ( البته در حالت متناهی ) . ولی مسئله یافتن الگوریتمی برای ساختنِ گراف نیست، بلکه ما می خواهیم هر الگوریتمی نتیجه یکسان داشته باشد ( خالی از لطف نیست اگر خواننده سعی کند با کارت های شکل ( ۱ ) گراف را بسازد ) .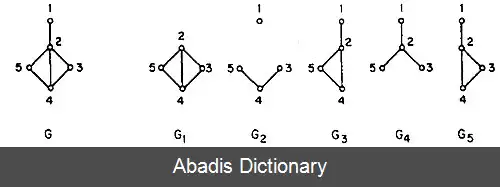
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر این بخش ما مقدمه و تاریخچه ای مختصر از حدس بازسازی گراف را از سال ۱۹۴۱ بیان می کنیم. حدس بازسازی ادعا می کند که هر گراف ساده با حداقل ۳ رأس از روی زیرگراف های رأس حذفی آن با تقریب یکریختی قابل بازسازی است. [ ۱]
حدس بازسازی یکی از مشهورترین مسایل نظریهٔ گراف است، که همواره ذهن بسیاری از ریاضی دانان را به خود مشغول کرده است. هراری[ ۲] از این مسئله به خاطر ماهیت مسری آن به عنوان بیماری گرافی یاد می کرد. بر اساس گزارش های ثبت شده، ویسکُنسین در ۱۹۴۱، کِلی و اُلام به عنوان اولین قربانیان این بیماری شناخته می شوند. نمادها با توجه به نمادگذاری کتابِ باندی و مورتی[ ۳] انتخاب شده است؛ بنابراین گراف G دارای مجموعه رأس های V ( G ) , مجموعه یال های E ( G ) ؛ همچنین دارای v ( G ) رأس و ε ( G ) یال است. زیرگراف G v زیرگراف حاصل از حذف رأسِ v به همراهِ تمام یال های متصل به آن است. شکل ( ۱ ) زیرگراف های رأس حذفی گراف G را نشان می دهد.
برای فرمول بندی دقیق حدس نیاز به دو مفهوم زیر داریم:
یک بازسازی از گراف G ، یک گراف H است، به طوری که V ( G ) = V ( H ) و برای هر v ∈ V ( G ) ، داشته باشیم H v ≅ G v . همچنین می گوییم G قابل بازسازی است، اگر هر بازسازی از G با خود G یکریخت باشد.
به عنوان مثال K 2 و 2 K 1 بازسازی یکدیگرند. حدس بازسازی ادعا می کند این دو، تنها گراف های غیرقابل بازسازی هستند.
• حدس بازسازی:[ ۴] [ ۵] تمام گراف های متناهی، ساده و غیرجهت دار با حداقل سه رأس قابل بازسازی هستند.
نگاه به مسئله به عنوان کارت هایی که هر زیرگراف روی آن ها رسم شده، خالی از لطف نیست. به طور نمونه گراف G در شکل ( ۲ ) دارای دسته کارتی مانند شکل ( ۵ ) است ( ارائه، توسط هَراری[ ۶] ) . نمایش مسئله با کارت ها، به طوری که گراف هایی که کارت ها را تولید می کنند بیابیم بسیار مرسوم است ( البته در حالت متناهی ) . ولی مسئله یافتن الگوریتمی برای ساختنِ گراف نیست، بلکه ما می خواهیم هر الگوریتمی نتیجه یکسان داشته باشد ( خالی از لطف نیست اگر خواننده سعی کند با کارت های شکل ( ۱ ) گراف را بسازد ) .


wiki: حدس بازسازی
