در ریاضیات، بخصوص در نظریه ترتیب، جوین ( به انگلیسی: Join ) ، یک زیر مجموعه S از یک مجموعه پوست ( مجموعه جزئاً مرتب یا POSET ) P ، برابر سوپریمم ( کوچکترین کران بالایی ) زیر مجموعه S است و آن را با ∨ S نمایش می دهند. به طور مشابه، "میت" ( به انگلیسی: Meet ) زیرمجموعه S ، به صورت ∧ S نمایش داده شده که همان اینفیمم ( بزرگترین کران پایین ) آن مجموعه است. ∨ و ∧ یک زیرمجموعه از مجموعه جزئاً مرتب لزوماً موجود نیستند. ∨ و ∧ دوگان یکدیگر اند.
مجموعه جزئاً مرتبی که تمام زوج اعضاء در آن دارای ∨ باشند را جوین - نیم - مشبکه گویند. دوگان آن میت - نیم - مشبکه است که برای تمام زوج اعضاء آن ∧ موجود است. یک مجموعه جزئاً مرتبی که هم جوین - نیم - مشبکه باشد و هم میت - نیم - مشبکه باشد را مشبکه گویند. مشبکه ای که در آن هر زیرمجموعه، و نه فقط هر جفت از اعضاء در آن دارای میت و جوین باشد را مشبکه کامل نامند. همچنین می توان مشبکه جزئی را تعریف کرد که در آن تمام زوج اعضاء لزوماً میت و جوین ندارند اما عملیاتی که در آن تعریف می شود باید در اصول موضوعه هایی صدق کنند. [ ۱]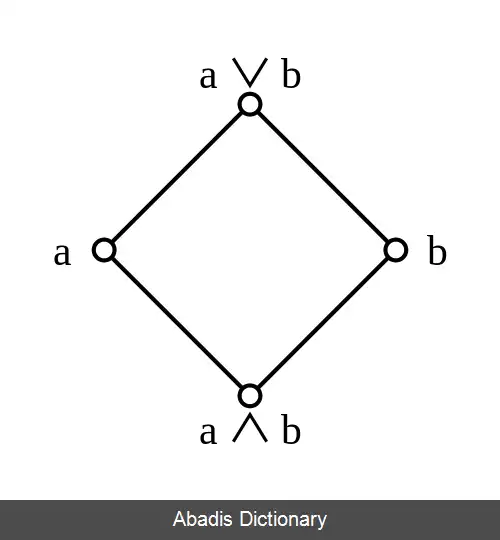
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمجموعه جزئاً مرتبی که تمام زوج اعضاء در آن دارای ∨ باشند را جوین - نیم - مشبکه گویند. دوگان آن میت - نیم - مشبکه است که برای تمام زوج اعضاء آن ∧ موجود است. یک مجموعه جزئاً مرتبی که هم جوین - نیم - مشبکه باشد و هم میت - نیم - مشبکه باشد را مشبکه گویند. مشبکه ای که در آن هر زیرمجموعه، و نه فقط هر جفت از اعضاء در آن دارای میت و جوین باشد را مشبکه کامل نامند. همچنین می توان مشبکه جزئی را تعریف کرد که در آن تمام زوج اعضاء لزوماً میت و جوین ندارند اما عملیاتی که در آن تعریف می شود باید در اصول موضوعه هایی صدق کنند. [ ۱]

wiki: جوین و میت
